Texas Instruments (TI) Calculators for Probability Distributions

Samuel Dominic Chukwuemeka (SamDom For Peace)

You may use any of these TI calculators:
TI-83 Plus
TI-84 Plus series
TI-Nspire CX series
TI-89 Titanium
TI-73 Explorer

Notable Notes
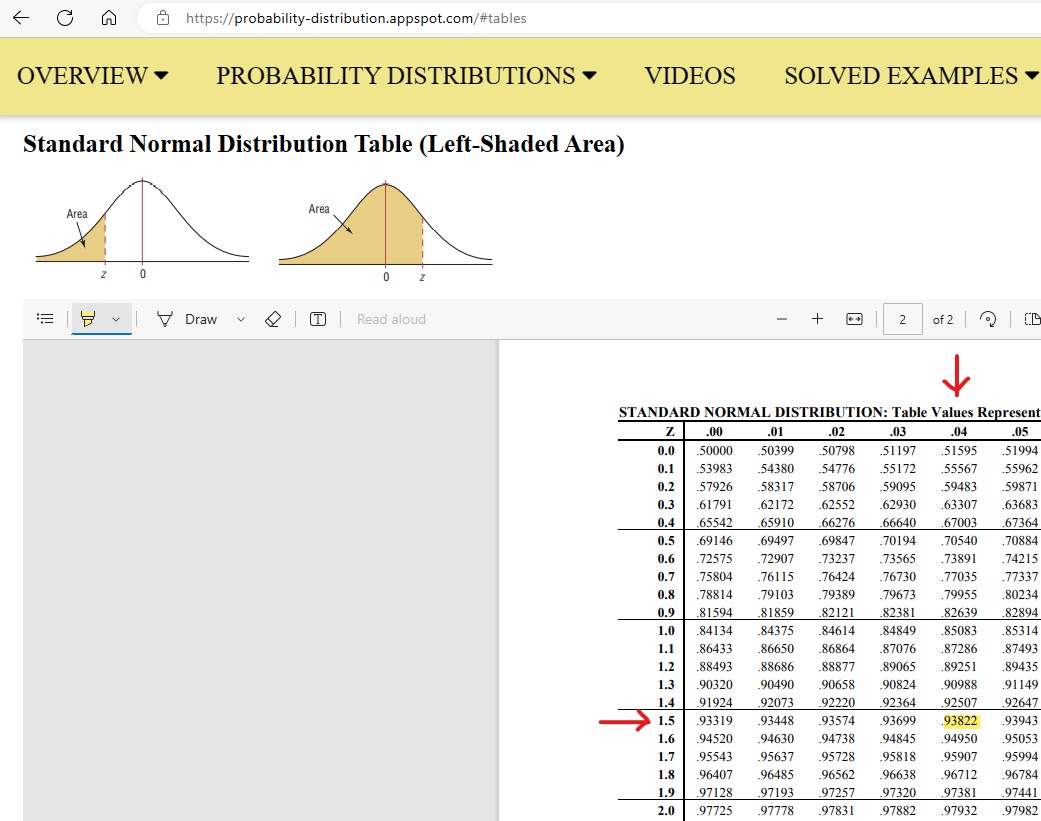
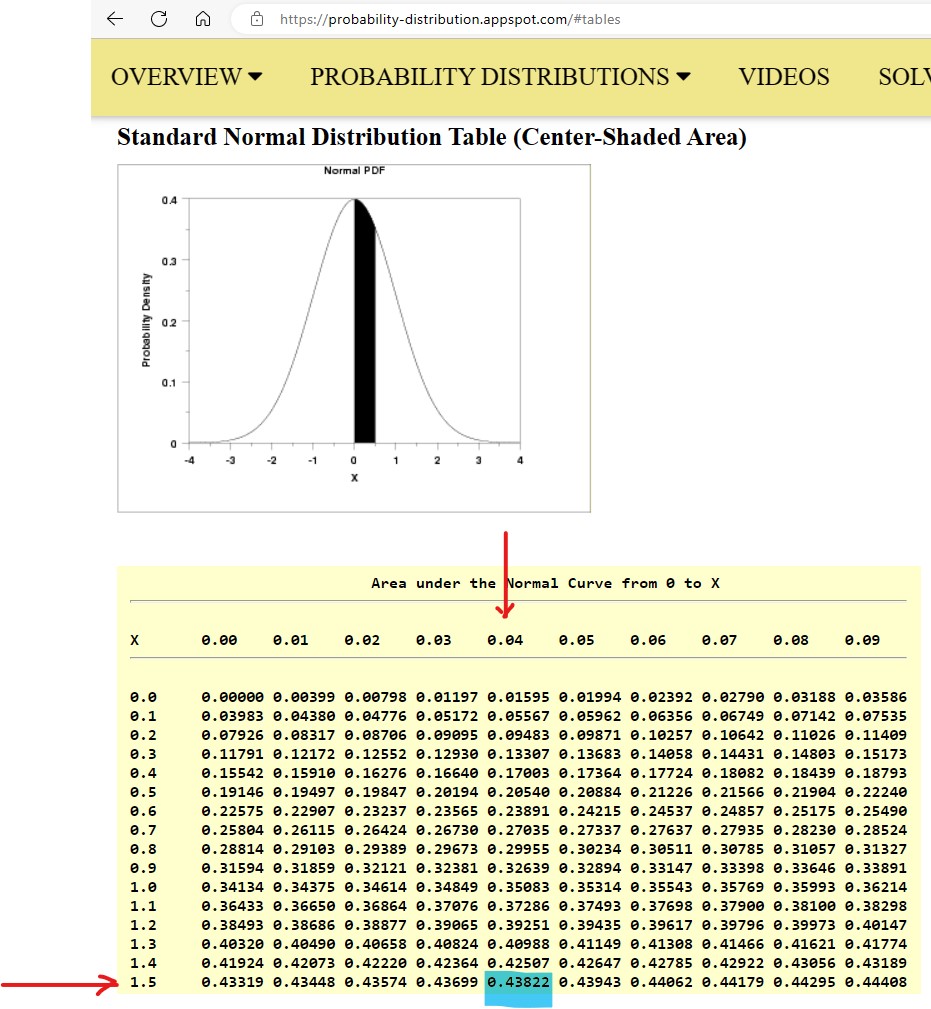
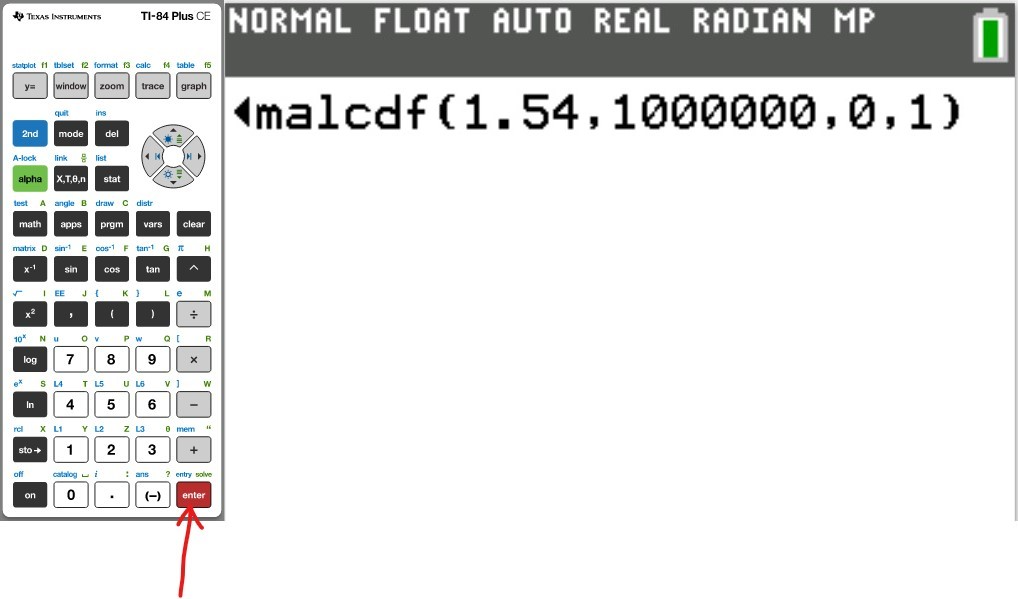
(1.) To find the probability of any probability distribution, use the distribution function DISTR
Because this is in blue color, it can be assessed after 2ND function button is pressed (because the 2ND function button is blue)

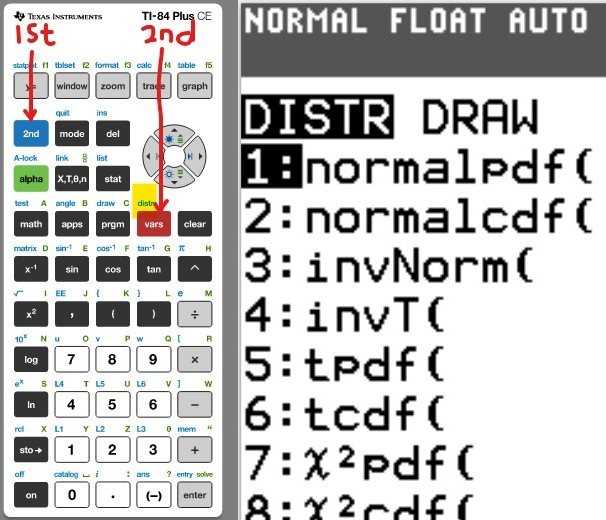
First Step

(2.) For Normal Distribution:
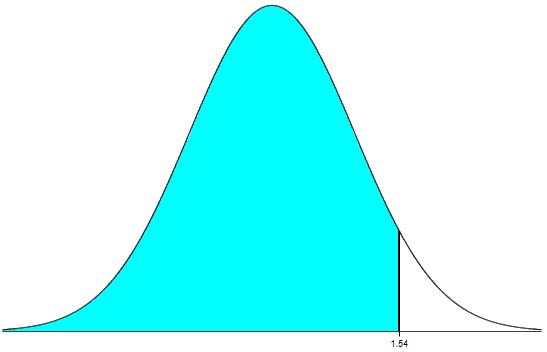
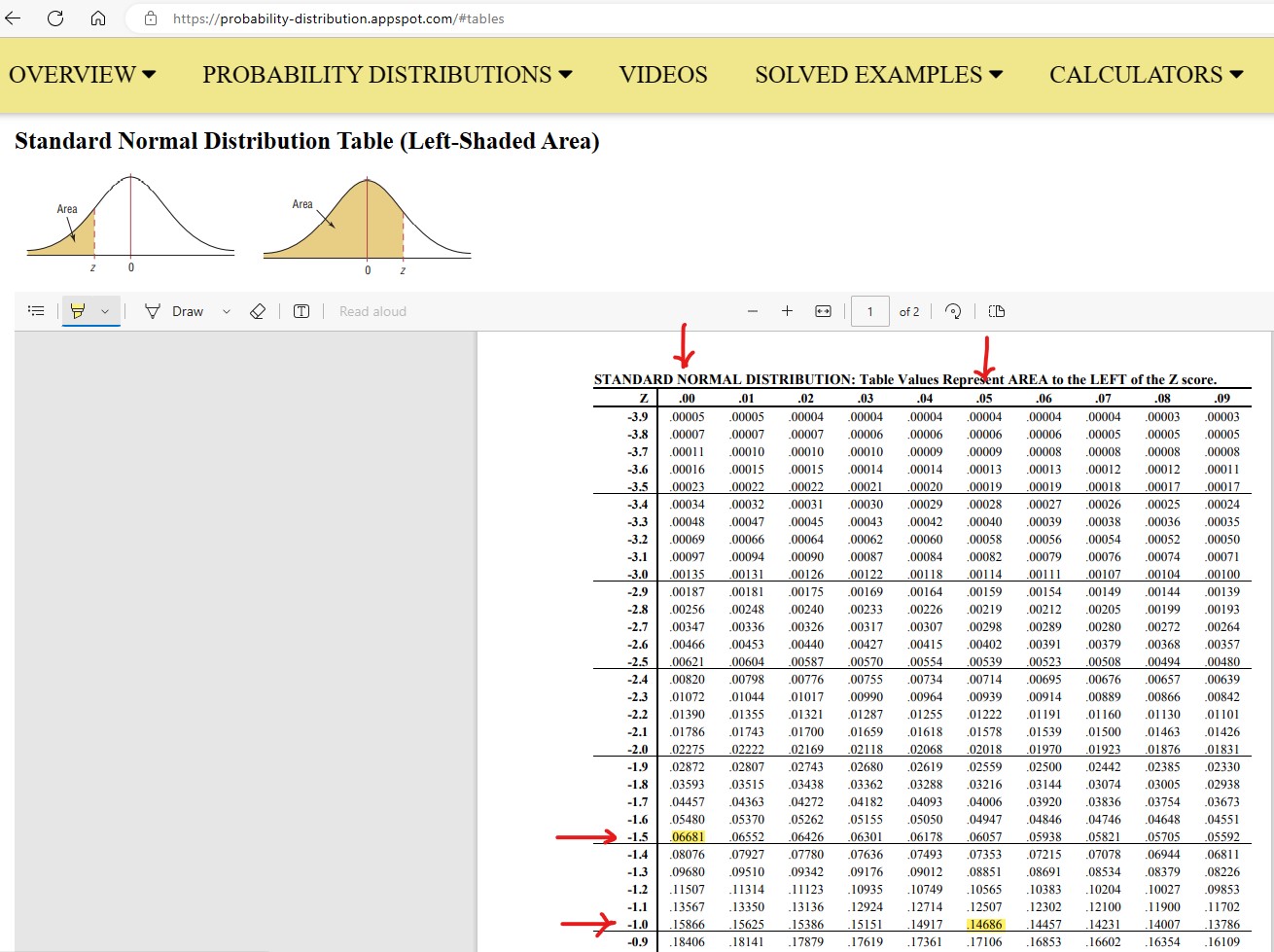
(a.) To find the area or percentage or probability: (i.) less than or equal to a certain value (at most the certain value)
(ii.) more than or equal to a certain value (at least the certain value)
(iii.) between two values
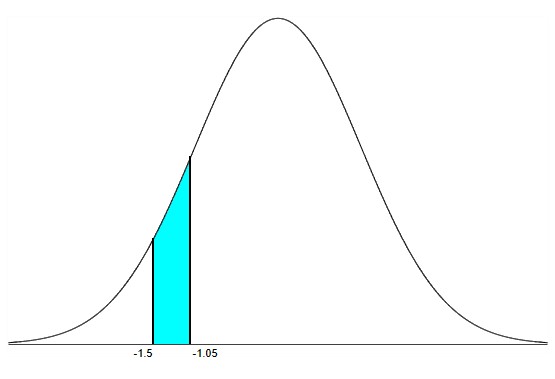
(iv.) away from two values
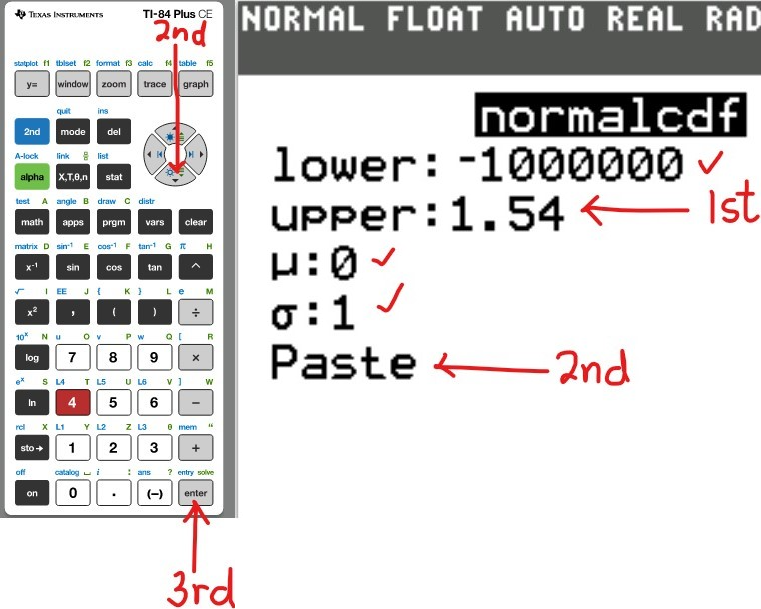
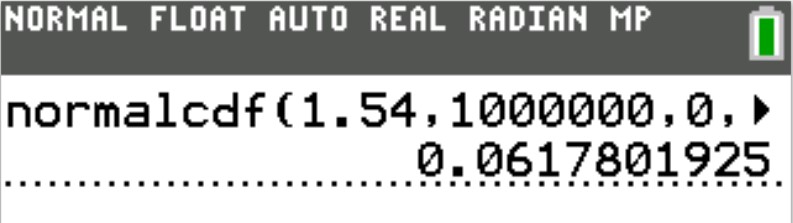
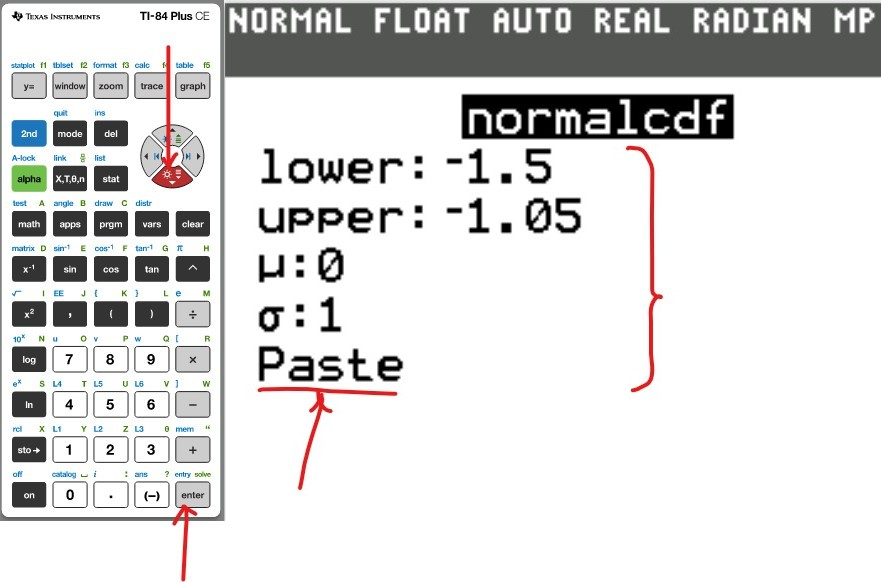
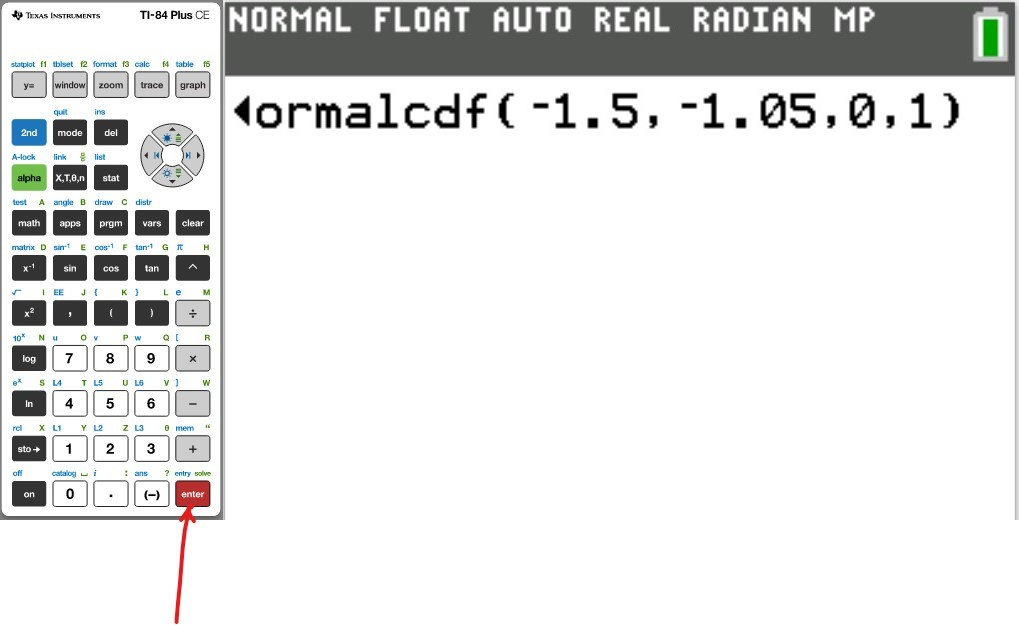
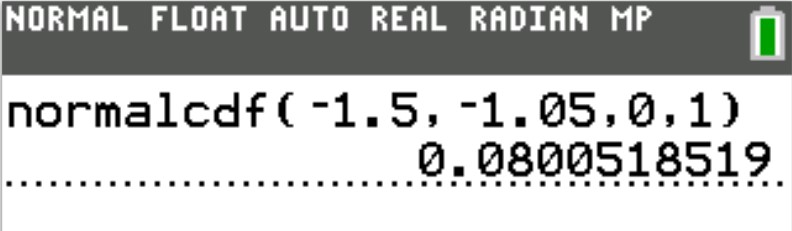
Use the normalcdf (Normal Cumulative Distribution) function

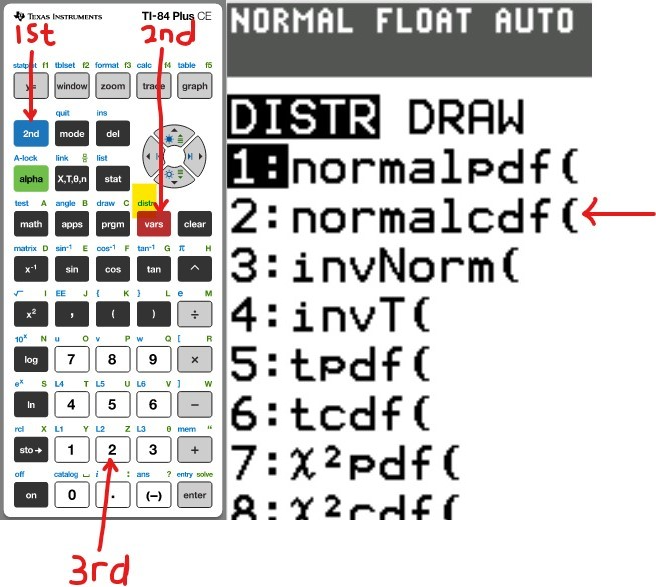
Second Step

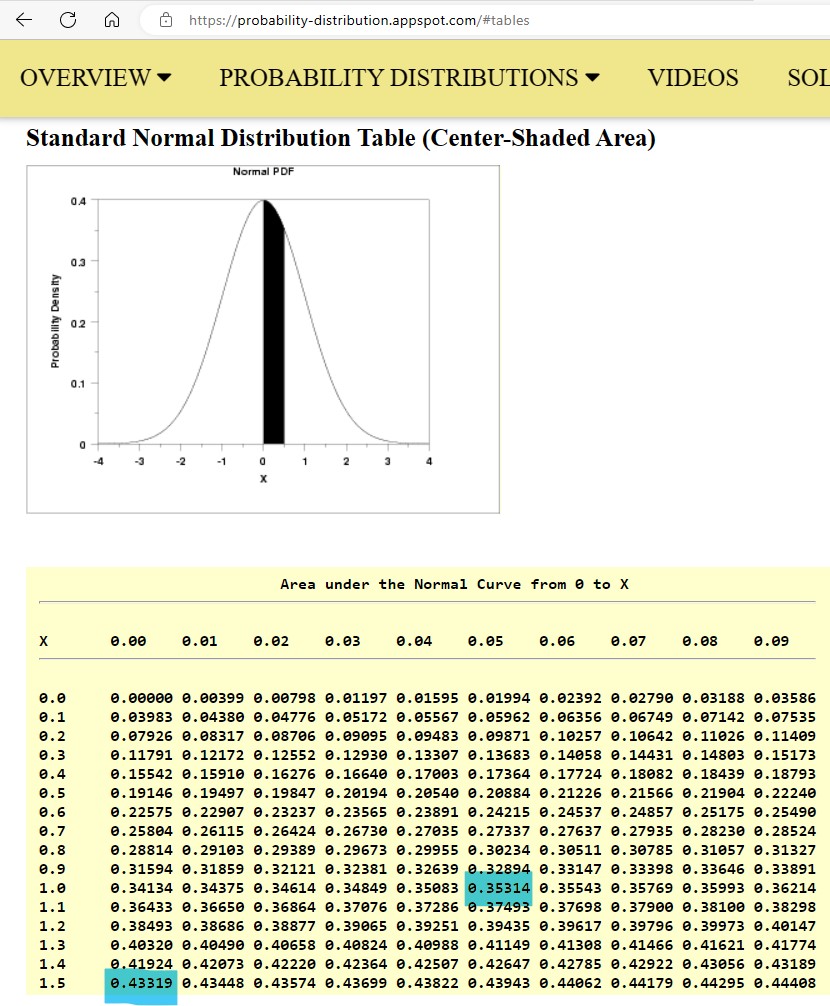
(b.) To find the area or percentage or probability: less than or equal to a certain value (at most the certain value):
(i.) set the lower: −1000000
(ii.) set the upper: certain value

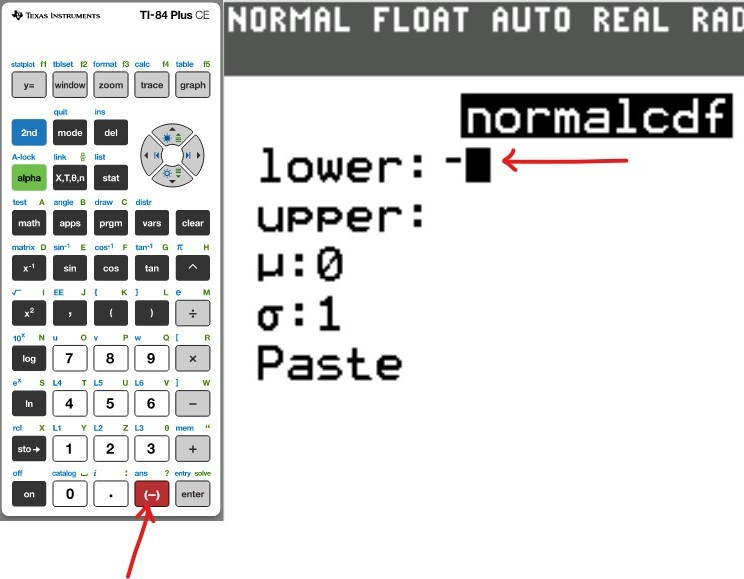
Second Step: (a)

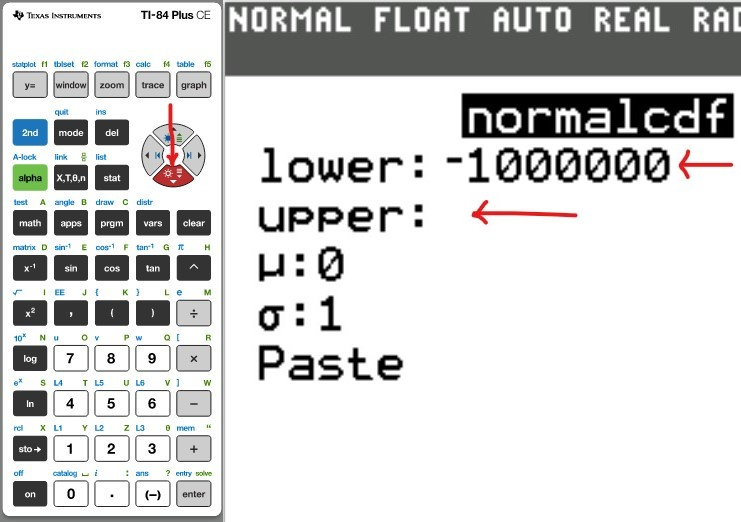
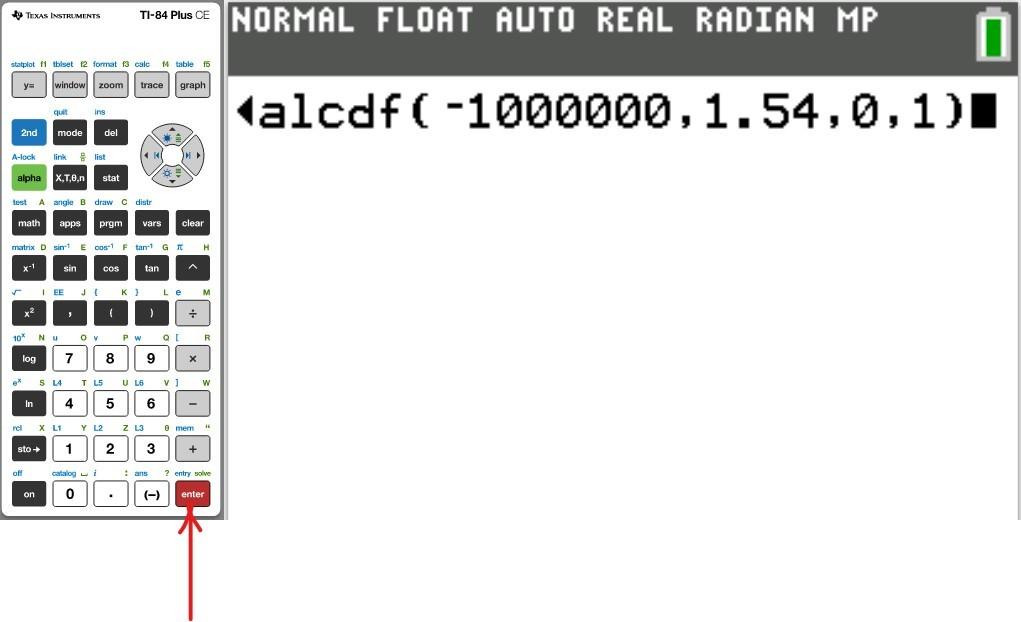
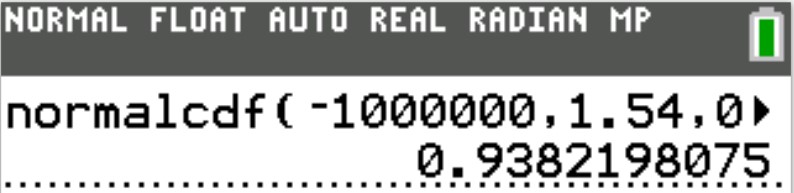
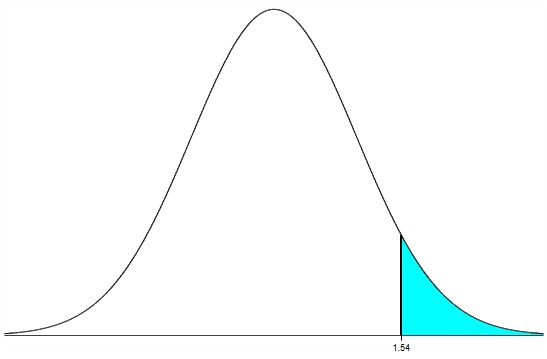
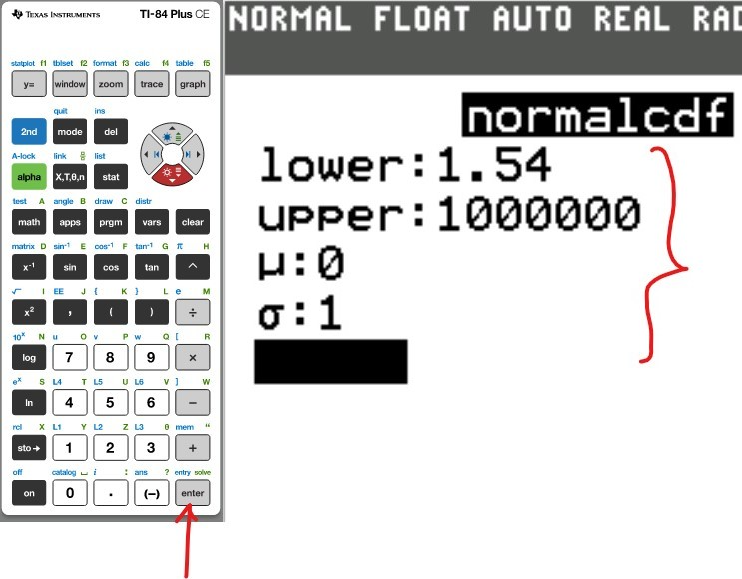
(c.) To find the area or percentage or probability: greater than or equal to a certain value (at least the certain value):
(i.) set the lower: certain value
(ii.) set the upper: 1000000

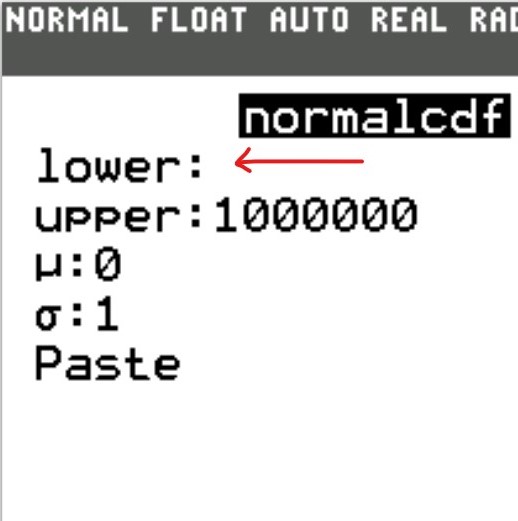
Second Step: (c)

(d.) To find the area or percentage or probability between two values:
(i.) set the lower: first value
(ii.) set the upper: second value

(e.) To find the area or percentage or probability away from two values:
(i.) set the lower: −1000000
(ii.) set the upper: first value
Added to
(iii.) set the lower: second value
(iv.) set the upper: 1000000

(3.) To find the inverse of any probability distribution, use the distribution function DISTR
Because this is in blue color, it can be assessed after 2ND function button is pressed (because the 2ND function button is blue)

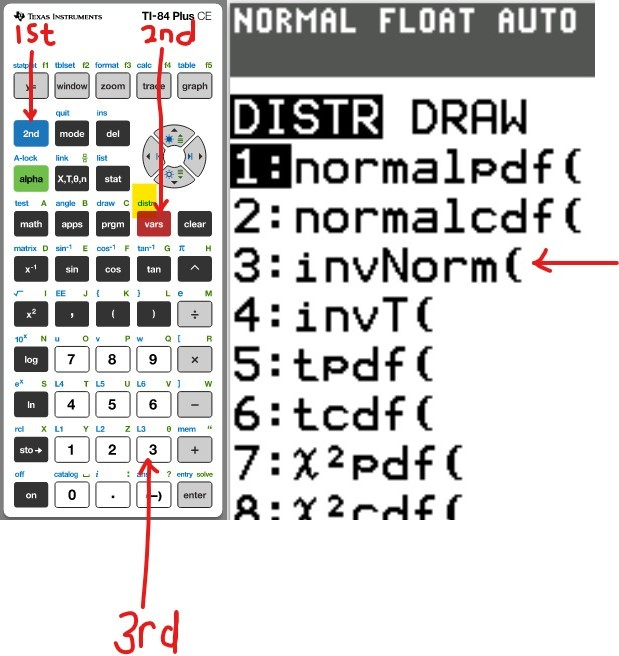
Third Step

(4.)

Let us do some examples.
NOTE: Please begin from the first example. Do not skip.

(a.) The graph that shows the probability that a z-score is 1.54 or less is option D.
Number 11a

(b.) 1.54 = 1.5 (vertical); 0.04 (horizontal)

First Approach: Left-Shaded Area
Number 11b-1st

The probability that a z-score will be 1.54 or less = P(z ≤ 1.54)
= 0.93822 ≈ 0.9382

Second Approach: Center-Shaded Area
Number 11b-2nd

The probability that a z-score will be 1.54 or less
= P(z ≤ 1.54)
= 0.5 + 0.43822
= 0.93822 ≈ 0.9382

Third Approach: Texas Instruments (TI) technology
Please see screenshots below.
The probability that a z-score will be 1.54 or less
= 0.9382198075 ≈ 0.9382

(c.) The graph that shows the probability that a z-score is 1.54 or more is option B.
Number 11c

(d.) First Approach: Left-Shaded Area
The probability that a z-score will be 1.54 or more
= P(z ≥ 1.54)
= 1 − 0.93822
= 0.06178 ≈ 0.0618

Second Approach: Center-Shaded Area
Number 11b-2nd

The probability that a z-score will be 1.54 or more
= P(z ≥ 1.54)
= 0.5 − 0.43822
= 0.06178 ≈ 0.0618

Third Approach: Texas Instruments (TI) technology
Please see screenshots below.
The probability that a z-score will be 1.54 or more
= 0.0617801925 ≈ 0.0618

(e.) The graph that shows the probability that a z-score is between −1.5 and −1.05 is option A.
Number 11e

(f.) −1.5 = −1.5 (vertical); 0.00 (horizontal)
−1.05 = −1.0 (vertical); 0.05 (horizontal)

First Approach: Left-Shaded Area
Number 11f-1st

The probability that a z-score is between −1.5 and −1.05
= P(−1.5 ≤ z ≤ −1.05)
= P(z ≤ −1.05) - P(z ≤ −1.5)
= 0.14686 − 0.06681
= 0.08005 ≈ 0.0801

Second Approach: Center-Shaded Area
Number 11f-2nd

The probability that a z-score is between −1.5 and −1.05
= P(−1.5 ≤ z ≤ −1.05)
= P(0 ≤ z ≤ −1.5) − = P(0 ≤ z ≤ −1.05)...symmetrical
= 0.43319 − 0.35314
= 0.08005 ≈ 0.0801

Third Approach: Texas Instruments (TI) technology
Please see screenshots below.
The probability that a z-score is between −1.5 and −1.05
= 0.080018519 ≈ 0.0801