(1.) Chloe wants to go skiing tomorrow, but only if there are 4 inches or more of new snow.
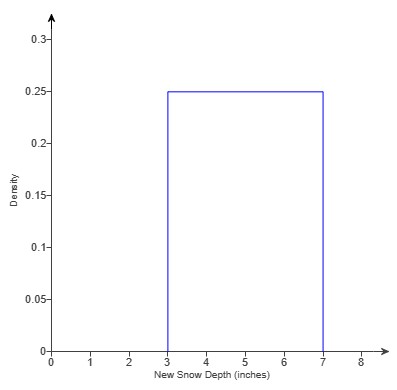
According to the weather report, any amount of new snow between 3 inches and 7 inches is equally likely.
The probability density curve for tomorrow's new snow depth is shown.
Find the probability that the new snow depth will be inches or more tomorrow.
Copy the graph, shade the appropriate area, and calculate its numerical value to find the probability.
The total area is 1.
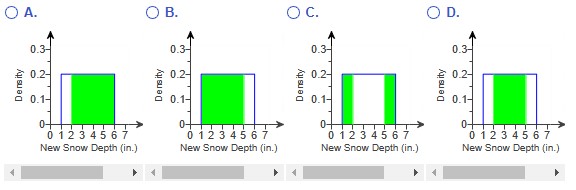
(a.) Shade the area of the graph that represents the likelihood of 4 or more inches of new snow.
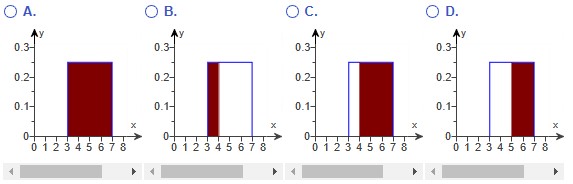
(b.) What is the probability that there will be 4 or more inches of new snow?
(a.) The shaded area of the graph that represents the likelihood of 4 or more inches of new snow is: Option C.
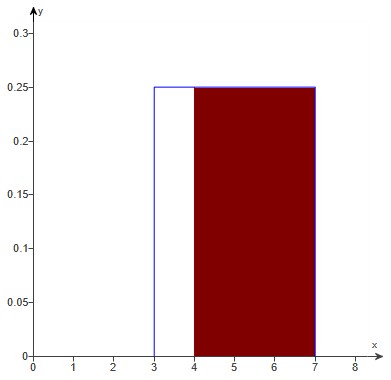
(b.) From 3 to 7 is 4 parts
3 to 4 is one part
4 to 5 is one part
5 to 6 is one part
6 to 7 is one part
The total area is 1
This implies that each part is $\dfrac{1}{4} = 0.25$
We shaded 3 out of 4 parts
Therefore:
$ P(\ge 4\;\;inches\;\;of\;\;snow) \\[3ex] = 0.25 + 0.25 + 0.25 \\[3ex] = 0.75 $
According to the weather report, any amount of new snow between 3 inches and 7 inches is equally likely.
The probability density curve for tomorrow's new snow depth is shown.
Find the probability that the new snow depth will be inches or more tomorrow.
Copy the graph, shade the appropriate area, and calculate its numerical value to find the probability.
The total area is 1.

(a.) Shade the area of the graph that represents the likelihood of 4 or more inches of new snow.

(b.) What is the probability that there will be 4 or more inches of new snow?
(a.) The shaded area of the graph that represents the likelihood of 4 or more inches of new snow is: Option C.

(b.) From 3 to 7 is 4 parts
3 to 4 is one part
4 to 5 is one part
5 to 6 is one part
6 to 7 is one part
The total area is 1
This implies that each part is $\dfrac{1}{4} = 0.25$
We shaded 3 out of 4 parts
Therefore:
$ P(\ge 4\;\;inches\;\;of\;\;snow) \\[3ex] = 0.25 + 0.25 + 0.25 \\[3ex] = 0.75 $
(2.)