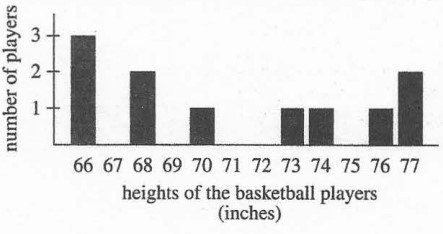
(31.) ACT Ms. Simons made a bar graph of the $20$ scores on the last math test, as shown below.
Which of the following statements about the mean of the $20$ scores is true?
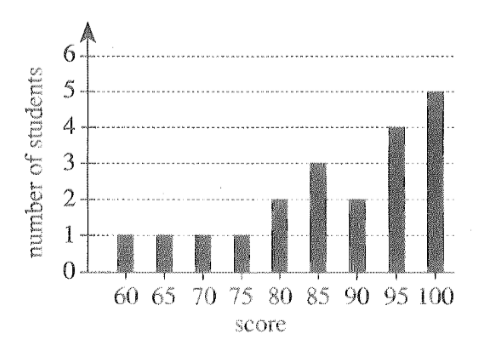
F. The mean is less than $75$
G. The mean is $75$
H. The mean is between $75$ and $85$
J. The mean is $85$
K. The mean is greater than $85$
$ Based\:\:on\:\:the\:\:bar\:\:graph \\[1em] 1\:\:student\:\:scored\:\:60 \\[1em] 1\:\:student\:\:scored\:\:65 \\[1em] 1\:\:student\:\:scored\:\:70 \\[1em] 1\:\:student\:\:scored\:\:75 \\[1em] 2\:\:students\:\:scored\:\:80 \\[1em] 3\:\:students\:\:scored\:\:85 \\[1em] 2\:\:students\:\:scored\:\:90 \\[1em] 4\:\:students\:\:scored\:\:95 \\[1em] 5\:\:students\:\:scored\:\:100 \\[1em] Number\:\:of\:\:students = 1 + 1 + 1 + 1 + 2 + 3 + 2 + 4 + 5 = 20\:\:students...to\:\:confirm\:\:20\:\:scores \\[1em] $
$ \bar{x} = \dfrac{\Sigma fx}{\Sigma f} \\[5ex] \bar{x} = \dfrac{1745}{20} \\[5ex] \bar{x} = 87.25 \\[1em] 87.25 \gt 85 $
Which of the following statements about the mean of the $20$ scores is true?

F. The mean is less than $75$
G. The mean is $75$
H. The mean is between $75$ and $85$
J. The mean is $85$
K. The mean is greater than $85$
$ Based\:\:on\:\:the\:\:bar\:\:graph \\[1em] 1\:\:student\:\:scored\:\:60 \\[1em] 1\:\:student\:\:scored\:\:65 \\[1em] 1\:\:student\:\:scored\:\:70 \\[1em] 1\:\:student\:\:scored\:\:75 \\[1em] 2\:\:students\:\:scored\:\:80 \\[1em] 3\:\:students\:\:scored\:\:85 \\[1em] 2\:\:students\:\:scored\:\:90 \\[1em] 4\:\:students\:\:scored\:\:95 \\[1em] 5\:\:students\:\:scored\:\:100 \\[1em] Number\:\:of\:\:students = 1 + 1 + 1 + 1 + 2 + 3 + 2 + 4 + 5 = 20\:\:students...to\:\:confirm\:\:20\:\:scores \\[1em] $
| Scores, $x$ | Frequencies, $f$ | $f * x$ |
| $60$ | $1$ | $60$ |
| $65$ | $1$ | $65$ |
| $70$ | $1$ | $70$ |
| $75$ | $1$ | $75$ |
| $80$ | $2$ | $160$ |
| $85$ | $3$ | $255$ |
| $90$ | $2$ | $180$ |
| $95$ | $4$ | $380$ |
| $100$ | $5$ | $500$ |
| $\Sigma f = 20$ | $\Sigma fx = 1745$ |
$ \bar{x} = \dfrac{\Sigma fx}{\Sigma f} \\[5ex] \bar{x} = \dfrac{1745}{20} \\[5ex] \bar{x} = 87.25 \\[1em] 87.25 \gt 85 $
(32.) ACT Set A and Set B each consist of $5$ distinct numbers.
The $2$ sets contain identical numbers with the exception of the number with the least value in each set.
The number with the least value in Set B is greater than the number with the least value in Set A.
The value of which of the following measures must be greater for Set B than for Set A?
A. Mean only
B. Median only
C. Mode only
D. Mean and median only
E. Mean, median, and mode
Let us write the two sets and ensure that the elements of the sets are listed in ascending order (from least to greatest).
We write these sets based on the information we were given.
Assume that:
$ A = \{1, 3, 4, 5, 6\} \\[1em] B = \{2, 3, 4, 5, 6\}...2 \gt 1 \\[1em] Median\:\:is\:\:the\:\:same = 4 \\[1em] Mode\:\:is\:\:the\:\:same...no\:\:mode \\[1em] Mean\:\:is\:\:different \\[1em] Mean\:\:of\:\:Set\:B \gt Mean\:\:of\:\:Set\: A \\[1em] How? \\[1em] \bar{x}\:\:of\:\:Set\:B = \dfrac{2 + 3 + 4 + 5 + 6}{5} = \dfrac{20}{5} = 4 \\[2em] \bar{x}\:\:of\:\:Set\:A = \dfrac{1 + 3 + 4 + 5 + 6}{5} = \dfrac{19}{5} \lt 4 $
The $2$ sets contain identical numbers with the exception of the number with the least value in each set.
The number with the least value in Set B is greater than the number with the least value in Set A.
The value of which of the following measures must be greater for Set B than for Set A?
A. Mean only
B. Median only
C. Mode only
D. Mean and median only
E. Mean, median, and mode
Let us write the two sets and ensure that the elements of the sets are listed in ascending order (from least to greatest).
We write these sets based on the information we were given.
Assume that:
$ A = \{1, 3, 4, 5, 6\} \\[1em] B = \{2, 3, 4, 5, 6\}...2 \gt 1 \\[1em] Median\:\:is\:\:the\:\:same = 4 \\[1em] Mode\:\:is\:\:the\:\:same...no\:\:mode \\[1em] Mean\:\:is\:\:different \\[1em] Mean\:\:of\:\:Set\:B \gt Mean\:\:of\:\:Set\: A \\[1em] How? \\[1em] \bar{x}\:\:of\:\:Set\:B = \dfrac{2 + 3 + 4 + 5 + 6}{5} = \dfrac{20}{5} = 4 \\[2em] \bar{x}\:\:of\:\:Set\:A = \dfrac{1 + 3 + 4 + 5 + 6}{5} = \dfrac{19}{5} \lt 4 $