(11.) A research poll showed that 1217 out of 2033 randomly polled people in a country favor the death
penalty for anyone convicted of murder.
Assume the conditions for the Central Limit Theorem were met.
Using the technology output below:

(a.) Interpret the confidence interval.
(b.) Is it plausible to claim that a majority favor the death penalty? Explain.
(a.) There is 95% confidence that the population proportion favoring the death penalty is between 0.577315 and 0.619930
(b.) Yes, it is a plausible claim because the confidence interval contains values above 50%.
Assume the conditions for the Central Limit Theorem were met.
Using the technology output below:

(a.) Interpret the confidence interval.
(b.) Is it plausible to claim that a majority favor the death penalty? Explain.
(a.) There is 95% confidence that the population proportion favoring the death penalty is between 0.577315 and 0.619930
(b.) Yes, it is a plausible claim because the confidence interval contains values above 50%.
(12.) When asked whether marriage is becoming obsolete, 759 out of 2034 randomly selected adults who
responded to a poll said yes.
Assume the conditions for the Central Limit Theorem were met.
Using the technology output below:
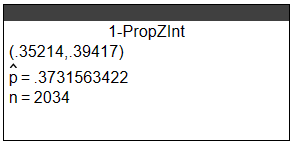
(a.) Report a 95% confidence interval for the proportion.
(b.) Is it plausible to claim that a majority think marriage is becoming obsolete?
(a.) With 95% confidence, the population proportion of people who think marriage is becoming obsolete is between 0.35214 and 0.39417
(b.) No, it is not a plausible claim because the confidence interval does not contain values above 50%.
Assume the conditions for the Central Limit Theorem were met.
Using the technology output below:

(a.) Report a 95% confidence interval for the proportion.
(b.) Is it plausible to claim that a majority think marriage is becoming obsolete?
(a.) With 95% confidence, the population proportion of people who think marriage is becoming obsolete is between 0.35214 and 0.39417
(b.) No, it is not a plausible claim because the confidence interval does not contain values above 50%.