Solved Examples: Probability Distributions

For ACT Students
The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for any wrong answer.

For WASSCE Students
Any question labeled WASCCE is a question for the WASCCE General Mathematics
Any question labeled WASSCE-FM is a question for the WASSCE Further Mathematics/Elective Mathematics

For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.

Solve all questions.
Show all work.

(1.) Samuel tossed a coin four times.
(a.) List the outcomes of his experiment.
(b.) List the random variable, $x$ for the number of tails in the outcomes.
(c.) Calculate the probability of the random variable, $P(x)$ for the outcomes.
(d.) Calculate the mean of the random variable.

We can use the Punnett Square or Tree Diagram to find the outcomes.
Let us use the Punnett Square.
You may choose to use Tree Diagram if you wish.
(a.)

2 coins on row, 2 coins on column
	HH	HT	TH	TT
HH	HHHH	HHHT	HHTH	HHTT
HT	HTHH	HTHT	HTTH	HTTT
TH	THHH	THHT	THTH	THTT
TT	TTHH	TTHT	TTTH	TTTT

(b.) and (c.)

$x$	$P(x)$	$x * P(x)$
$0$	$\dfrac{1}{16}$	$0$
$1$	$\dfrac{4}{16}$	$\dfrac{4}{16}$
$2$	$\dfrac{6}{16}$	$\dfrac{12}{16}$
$3$	$\dfrac{4}{16}$	$\dfrac{12}{16}$
$4$	$\dfrac{1}{16}$	$\dfrac{4}{16}$
$\Sigma x = 10$		$\Sigma[x * P(x)] = \dfrac{32}{16} = 2$

(d.)
$ \mu = \Sigma[x * P(x)] \\[3ex] \mu = \dfrac{32}{16} \\[5ex] \mu = 2 $

(2.) The table shows the random variable, $x$ and the probability of the random variable, $P(x)$

$x$	$0$	$1$	$2$	$3$
$P(x)$	$0.141$	$0.389$	$0.359$	$0.111$

The random variable represents the number of boys in a family with three children.
(a.) Calculate the mean of the random variable. Round to 2 decimal places.
(b.) Calculate the standard deviation of the random variable. Round to 2 decimal places.
(c.) Is it unusual for a family with three children to have only boys?

(a.)

$x$	$P(x)$	$x * P(x)$	$x^2$	$x^2 * P(x)$
$0$	$0.141$	$0$	$0$	$0$
$1$	$0.389$	$0.389$	$1$	$0.389$
$2$	$0.359$	$0.718$	$4$	$1.436$
$3$	$0.111$	$0.333$	$9$	$0.999$
$\Sigma[x * P(x)] = 1.44$			$\Sigma[x^2 * P(x)] = 2.824$

$ \mu = \Sigma[x * P(x)] \\[3ex] \mu = 1.44 \\[3ex] (b.) \\[3ex] \sigma = \sqrt{\Sigma[x^2 * P(x)] - \mu^2} \\[3ex] \sigma = \sqrt{2.824 - 1.44^2} \\[3ex] \sigma = \sqrt{2.824 - 2.0736} \\[3ex] \sigma = \sqrt{0.7504} \\[3ex] \sigma = 0.8662563131 \\[3ex] \sigma \approx 0.87 \\[3ex] (c.) \\[3ex] \underline{First\;\;Method:\;\;Probability} \\[3ex] P(3) = 0.111 \\[3ex] 0.111 \gt 5\% \\[3ex] 0.111 \gt 0.05 \\[3ex] $ Therefore, it is not unusual for a family with three children to have only boys.

$ \underline{Second\;\;Method:\;\;Usual\;\;Values} \\[3ex] Minimum\;\;usual\;\;value \\[3ex] = \mu - 2\sigma \\[3ex] = 1.44 - 2(0.8662563131) \\[3ex] = 1.44 - 1.732512626 \\[3ex] = -0.2925126262 \\[3ex] 3 \gt -0.2925126262 \\[3ex] Maximum\;\;usual\;\;value \\[3ex] = \mu - 2\sigma \\[3ex] = 1.44 + 2(0.8662563131) \\[3ex] = 1.44 + 1.732512626 \\[3ex] = 3.172512626 \\[3ex] 3 \lt 3.172512626 \\[3ex] -0.2925126262 \lt 3 \lt 3.172512626 \\[3ex] $ Therefore, it is not unusual for a family with three children to have only boys.

(3.) The table shows the results from groups of 10 births from 10 different sets of parents.

$x$	$P(x)$
$0$	$0.003$
$1$	$0.016$
$2$	$0.038$
$3$	$0.113$
$4$	$0.209$
$5$	$0.235$
$6$	$0.203$
$7$	$0.116$
$8$	$0.043$
$9$	$0.013$
$10$	$0.011$

The random variable, $x$ represents the number of girls among 10 children.
(a.) Using the Range Rule of Thumb, determine the maximum usual value.
(b.) Using the Range Rule of Thumb, determine the minimum usual value.
(c.) Based on the result, is 1 girl in 10 births an unusually low number of girls? Explain.

$x$	$P(x)$	$x * P(x)$	$x^2$	$x^2 * P(x)$
$0$	$0.003$	$0$	$0$	$0$
$1$	$0.016$	$0.016$	$1$	$0.016$
$2$	$0.038$	$0.076$	$4$	$0.152$
$3$	$0.113$	$0.339$	$9$	$1.017$
$4$	$0.209$	$0.836$	$16$	$3.344$
$5$	$0.235$	$1.175$	$25$	$5.875$
$6$	$0.203$	$1.218$	$36$	$7.308$
$7$	$0.116$	$0.812$	$49$	$5.684$
$8$	$0.043$	$0.344$	$64$	$2.752$
$9$	$0.013$	$0.117$	$81$	$1.053$
$10$	$0.011$	$0.110$	$100$	$1.100$
$\Sigma[x * P(x)] = 5.043$			$\Sigma[x^2 * P(x)] = 28.301$

$ \mu = \Sigma[x * P(x)] \\[3ex] \mu = 5.043 \\[3ex] \sigma = \sqrt{\Sigma[x^2 * P(x)] - \mu^2} \\[3ex] \sigma = \sqrt{28.301 - 5.043^2} \\[3ex] \sigma = \sqrt{28.301 - 25.431849} \\[3ex] \sigma = \sqrt{2.869151} \\[3ex] \sigma = 1.693856842 \\[3ex] (a.) \\[3ex] Maximum\;\;usual\;\;value \\[3ex] = \mu + 2\sigma \\[3ex] = 5.043 + 2(1.693856842) \\[3ex] = 5.043 + 3.387713683 \\[3ex] = 8.430713683 \\[3ex] (b.) \\[3ex] Minimum\;\;usual\;\;value \\[3ex] = \mu - 2\sigma \\[3ex] = 5.043 - 2(1.693856842) \\[3ex] = 5.043 - 3.387713683 \\[3ex] = 1.655286317 \\[3ex] (c.) \\[3ex] \underline{First\;\;Method:\;\;Probability} \\[3ex] P(1) = 0.016 \\[3ex] 0.016 \lt 5\% \\[3ex] 0.016 \lt 0.05 \\[3ex] $ Therefore, based on the result; 1 girl in 10 births is an unusually low number of girls.

$ \underline{Second\;\;Method:\;\;Usual\;\;Values} \\[3ex] 1 \lt 1.655286317 \\[3ex] $ Therefore, based on the result; 1 girl in 10 births is an unusually low number of girls.

(4.) Determine whether each of the following variables would best be modeled as continuous or discrete.
(a.) The exact time it takes to evaluate 57 + 75.
(b.) The time required to download a file from the internet.
(c.) Blood sugar level.
(d.) The weight of a T-bone steak.
(e.) The number of people with blood type B in a random sample of 52 people.
(f.) The length of time to run a marathon.
(g.) The number of fish caught during a fishing tournament.
(h.) The height of a randomly selected goat.
(i.) The number of science textbook authors.
(j.) The number of statistics students at BRCC.
(k.) The decibel level of a siren.
(m.) The number of mint condition baseballs cards.
(n.) The value of a pile of dimes.

Hint:
If you can count it, it is discrete.
If you can measure it, it is continuous.

(a.) The exact time it takes to evaluate 57 + 75.
The variable is continuous.

(b.) The time required to download a file from the internet.
The variable is continuous.

(c.) Blood sugar level.
The variable is continuous.

(d.) The weight of a T-bone steak.
The variable is continuous.

(e.) The number of people with blood type B in a random sample of 52 people.
The variable is discrete.

(f.) The number of free-throw attempts before the first shot is made.
The variable is discrete.

(g.) The number of fish caught during a fishing tournament.
The variable is discrete.

(h.) The height of a randomly selected goat.
The variable is continuous.

(i.) The number of science textbook authors.
The variable is discrete.

(j.) The number of statistics students at BRCC.
The variable is discrete.

(k.) The decibel level of a siren.
The variable is continuous.

(m.) The number of mint condition baseballs cards.
The variable is discrete.

(n.) The value of a pile of dimes. The variable is discrete.

(6.) The table shows the random variable, $x$ and the probability of the random variable, $P(x)$

$x$	$P(x)$
$0$	$0.000$
$1$	$0.003$
$2$	$0.016$
$3$	$0.054$
$4$	$0.121$
$5$	$0.193$
$6$	$0.226$
$7$	$0.193$
$8$	$0.121$
$9$	$0.054$
$10$	$0.016$
$11$	$0.003$
$12$	$0.000$

The random variable represents the number of Hispanics on a panel of 12 jury in a predominantly Hispanic population.
(a.) Determine the probability of having exactly 5 Hispanics among 12 jurors.
(b.) Determine the probability of having 5 or fewer Hispanics among 12 jurors.
(c.) Is 5 Hispanics an unusually low number of Hispanics among 12 jurors for that population?

$ (a.) \\[3ex] P(5) = 0.193 \\[3ex] (b.) \\[3ex] P(\le 5) = 0.000 + 0.003 + 0.016 + 0.054 + 0.121 + 0.193 \\[3ex] P(\le 5) = 0.387 \\[3ex] (c.) \\[3ex] 0.387 \gt 5\% \\[3ex] 0.387 \gt 0.05 \\[3ex] $ Hence, 5 Hispanics is not an unusually low number of Hispanics among 12 jurors for that population.

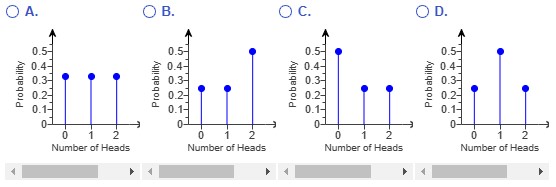
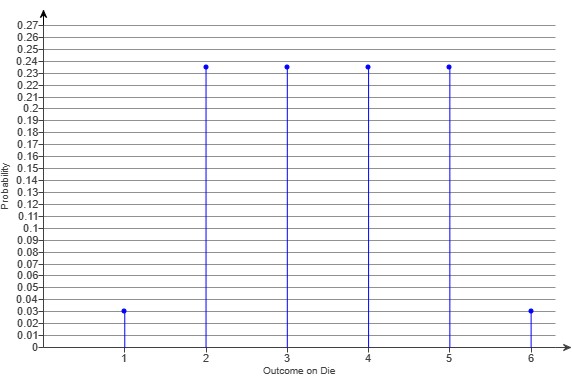
(7.) A gambler shaved an edge off one side of a six-sided die, and as a result, the die is no longer "fair."
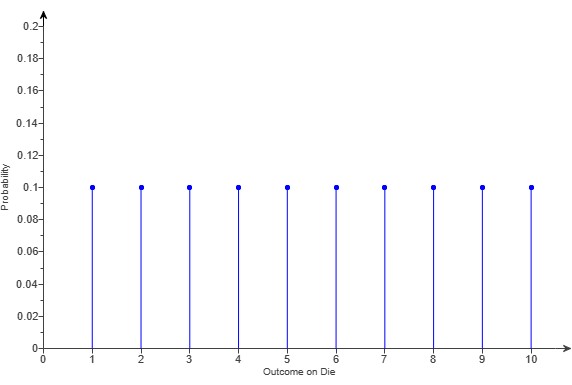
The figure shows a graph of the probability distribution function (pdf).
Show the pdf in table format by listing all six possible outcomes and their probabilities.

$ P(1) = P(6) = 0.03 \\[3ex] P(2) = P(3) P(4) = P(5) = k \\[3ex] \Sigma Probability = 1 \\[3ex] P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1 \\[3ex] 0.03 + k + k + k + k + 0.03 = 1 \\[3ex] 4k + 0.06 = 1 \\[3ex] 4k = 1 - 0.06 \\[3ex] 4k = 0.94 \\[3ex] k = \dfrac{0.94}{4} \\[5ex] k = 0.235 \\[3ex] $

Number of spots	1	2	3	4	5	6
Probability	0.03	0.235	0.235	0.235	0.235	0.03

(8.) Cardano plays lottery games.
If he picks a sequence of three digits from the numbers 0 through 9 in a lottery game, he will pay $1.35 because he has to pay $1.35 to play the game.
If he picks the same sequence of three digits in a drawing, he will win $487.75
(a.) How many different selections are possible?
(b.) Determine the probability of winning the lottery game
(c.) Calculate Cardano's net profit if he wins the lottery game
(d.) Calculate the expected value

(a.) The question did not specify whether the numbers can be picked: with or without repetition
The default is to assume that ghe numbers can be picked with repetition.
0 through 9 consists of 10 digits
$\underline{0 - 9}$ $\underline{0 - 9}$ $\underline{0 - 9}$
$\underline{10}$ $\underline{10}$ $\underline{10}$
Number of different selections
= $10 * 10 * 10
= 1000$ selections

$ (b.) \\[3ex] n(Winning) = 1 * 1 * 1 = 1 \\[3ex] n(S) = 10 * 10 * 10 = 1000 \\[3ex] P(Winning) = \dfrac{n(Winning)}{n(S)} \\[5ex] = \dfrac{1}{1000} \\[5ex] (c.) \\[3ex] Net\;\;profit = Winning\;\;amount - Amount\;\;to\;\;play \\[3ex] = 487.75 - 1.35 \\[3ex] = \$486.40 \\[3ex] $ (d.)

$ P(Winning) = \dfrac{1}{1000} \\[5ex] P(Losing) = 1 - P(Winning) ...Complementary\;\;Rule \\[3ex] P(Losing) \\[3ex] = 1 - \dfrac{1}{1000} \\[5ex] = \dfrac{1000}{1000} - \dfrac{1}{1000} \\[5ex] = \dfrac{1000 - 1}{1000} \\[5ex] = \dfrac{999}{1000} \\[5ex] $

Event	$x$	$P(x)$	$x * P(x)$
Lose the game	$-1.35$	$\dfrac{999}{1000}$	$-1.34865$
Win the game	$486.40$	$\dfrac{1}{1000}$	$0.4864$
$\Sigma[x * P(x)] = -0.86225$

$ E = \Sigma[x * P(x)] \\[3ex] E = -\$0.86225 \\[3ex] E \approx -\$0.86 $

(19.) Toss a fair ten-sided die.
The probability distribution function (pdf) in table form is given below.

Number of spots	1	2	3	4	5	6	7	8	9	10
Probability	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$	$\dfrac{1}{10}$

Make a graph of the pdf for the die.

Number 19

$ P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = P(7) = P(8) = P(9) = P(10) \\[3ex] = \dfrac{1}{10} \\[5ex] = 0.1 \\[3ex] $ The diagram is Option D.

Number 19

(20.) When a certain type of thumbtack is flipped, the probability of its landing tip up (U) is 0.55 and the probability of its landing tip down (D) is 0.45.
Suppose you flip two such thumbtacks, one at a time.
Make a list of all the possible arrangements using U for up and D for down.
Find the probabilities of each possible outcome.

$ S = {UU, UD, DU, DD} \\[3ex] with-replacement-condition \\[3ex] P(UU) = 0.55 * 0.55 = 0.3025 \\[3ex] P(UD) = 0.55 * 0.45 = 0.2475 \\[3ex] P(DU) = 0.45 * 0.55 = 0.2475 \\[3ex] P(DD) = 0.45 * 0.45 = 0.2025 $

Top

(21.) When a certain type of thumbtack is flipped, the probability of its landing tip up (U) is 0.55 and the probability of its landing tip down (D) is 0.45.
Suppose you flip two such thumbtacks, one at a time.
The probability distribution for the possible outcomes of these flips is shown below.

Outcomes	UU	UD	DU	DD
Probability	0.2916	0.2484	0.2484	0.2116

(a.) Find the probability of getting 0 ups, 1 up, or 2 ups when flipping two thumbtacks.
(b.) Make a probability distribution graph of this.

Number 21

One toss of two thumbsacks

$ P(0\;ups) = P(DD) = 0.2116 \\[5ex] P(exactly\;\;1\;up) \\[3ex] = P(UD\;\;or\;\;DU) \\[3ex] = P(UD) + P(DU) \\[3ex] = 0.2484 + 0.2484 \\[3ex] = 0.4968 \\[5ex] P(2\;ups) = P(UU) = 0.2916 \\[3ex] $ The probability distribution graph is: Option C.

Number 21

(23.) When a fair coin is flipped, the probability of its landing heads (H) is 0.50 and the probability of its landing tails (T) is also 0.50.
If a fair coin is flipped twice, the different possible arrangements would be HH, HT, TH, and TT.
The probability distribution of these arrangements is shown below.

Outcomes	HH	HT	TH	TT
Probability	0.25	0.25	0.25	0.25

(a.) Find the probability of getting 0 heads, 1 head, or 2 heads when flipping the coin twice.
(b.) Make a probability distribution graph of this.

Number 23

Two tosses of a fair coin

$ P(0\;heads) = P(TT) = 0.25 \\[5ex] P(exactly\;\;1\;head) \\[3ex] = P(HT\;\;or\;\;TH) \\[3ex] = P(HT) + P(TH) \\[3ex] = 0.25 + 0.25 \\[3ex] = 0.5 \\[5ex] P(2\;heads) = P(HH) = 0.25 \\[3ex] $ The probability distribution graph is: Option D.

Number 23

Top