R and RStudio for Descriptive Statistics

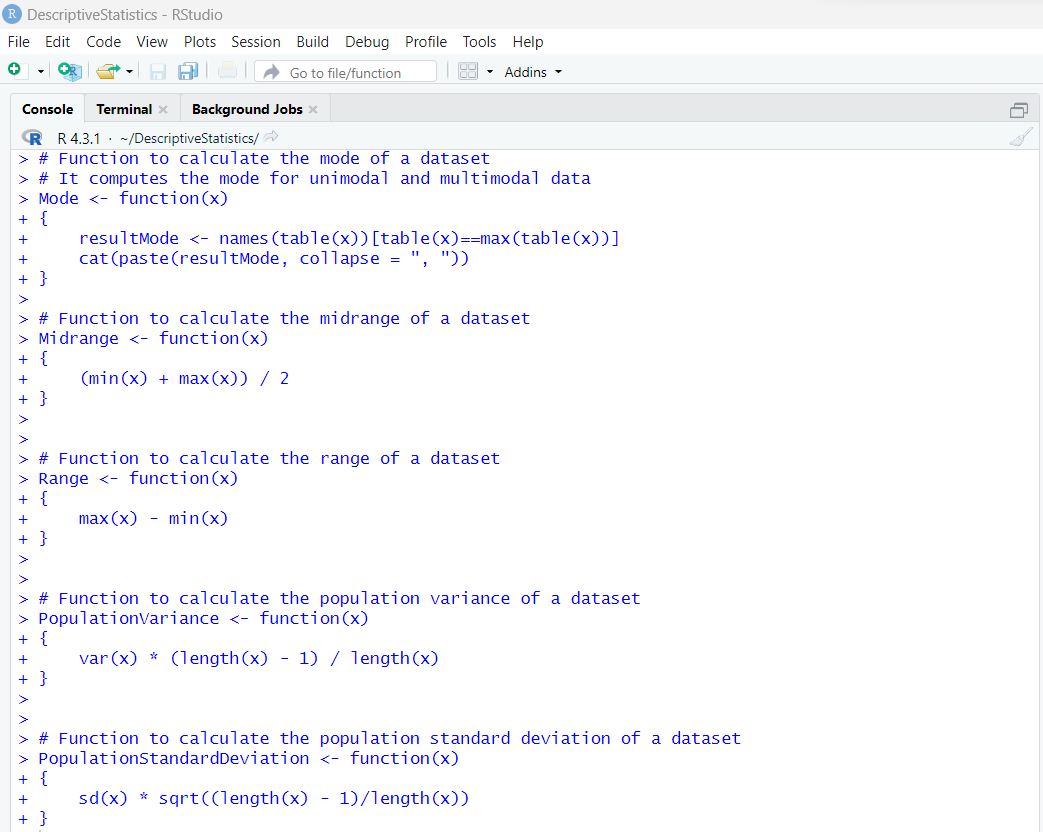
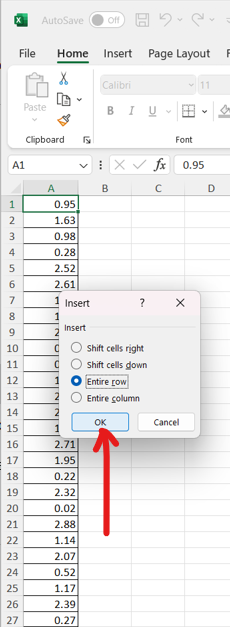
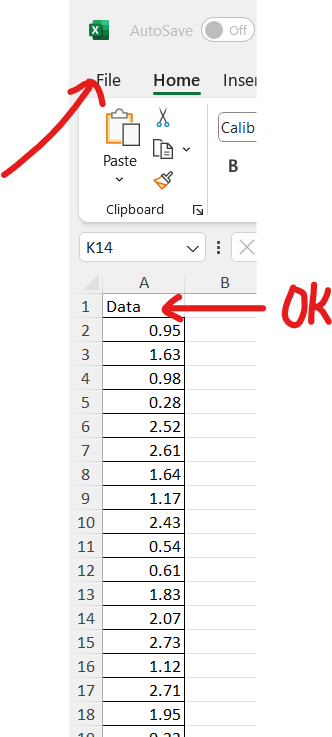
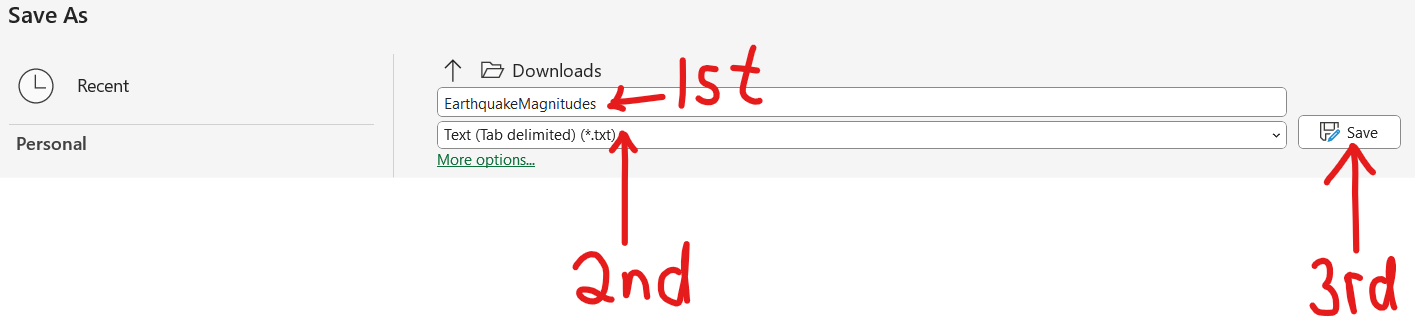
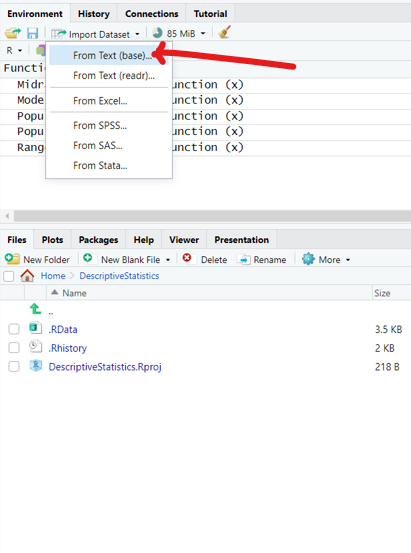
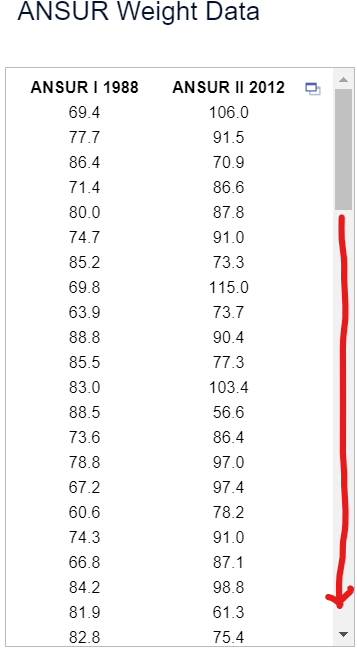
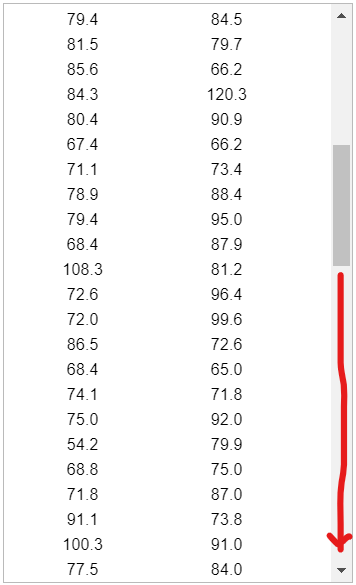
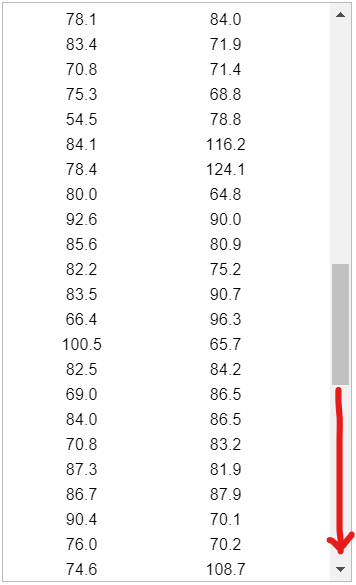
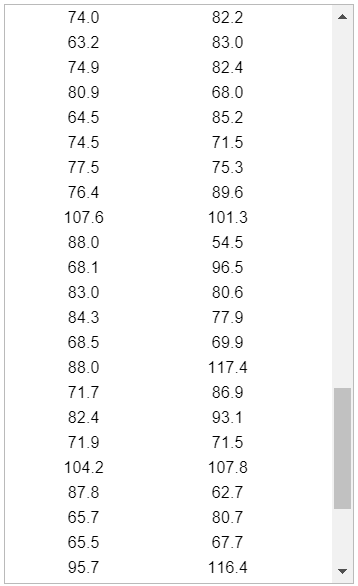
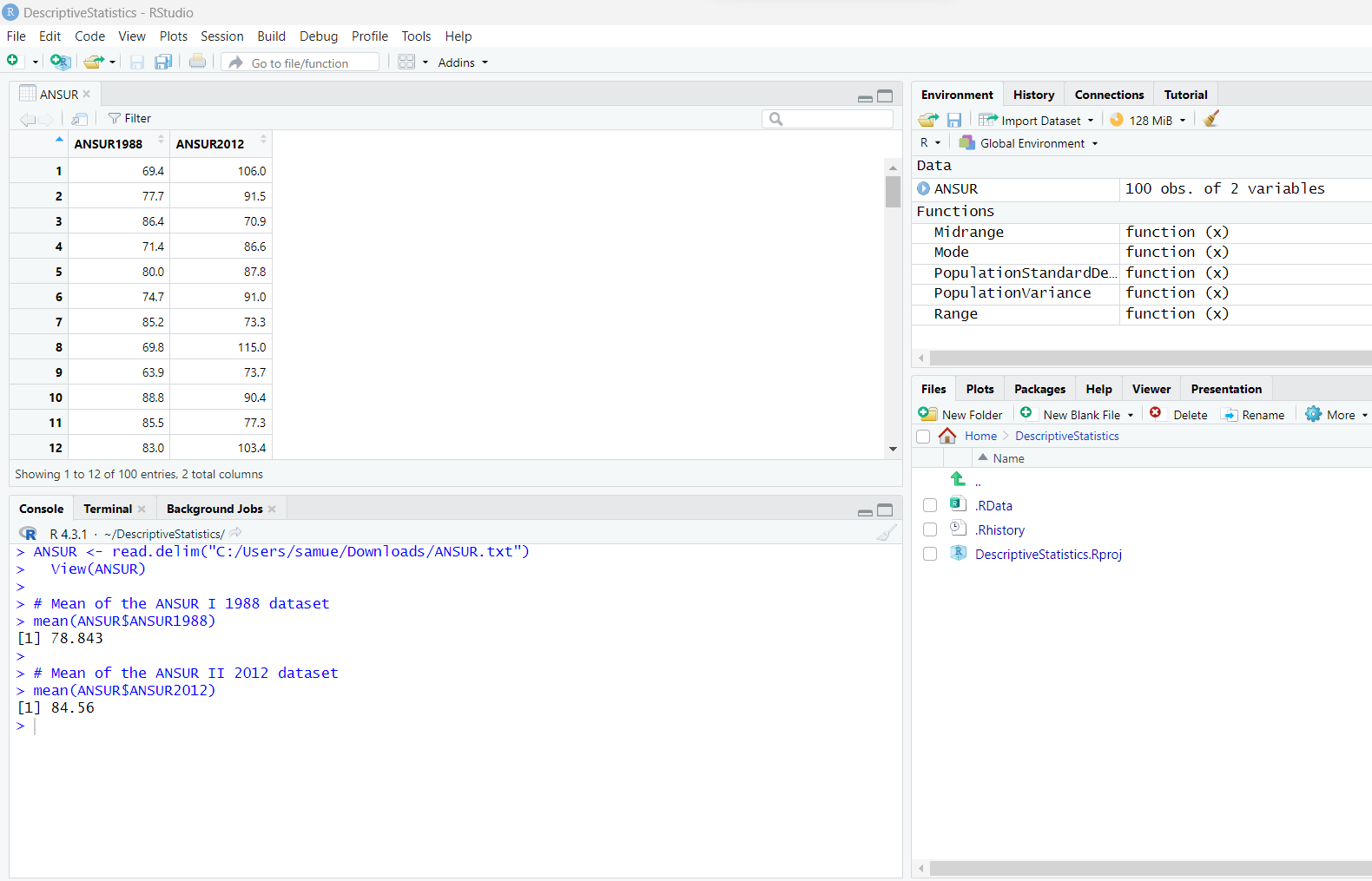
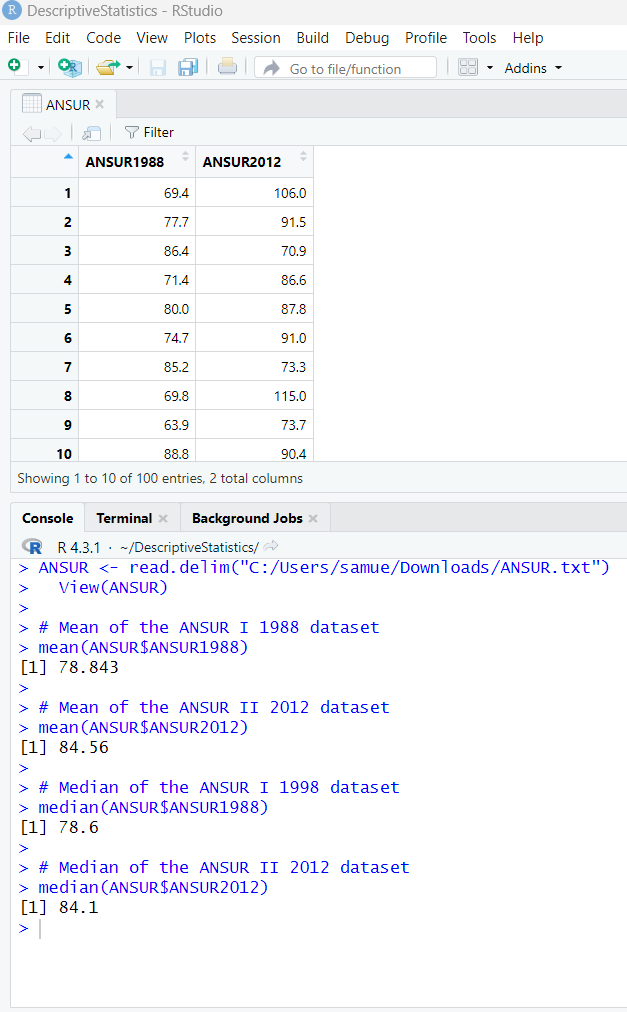
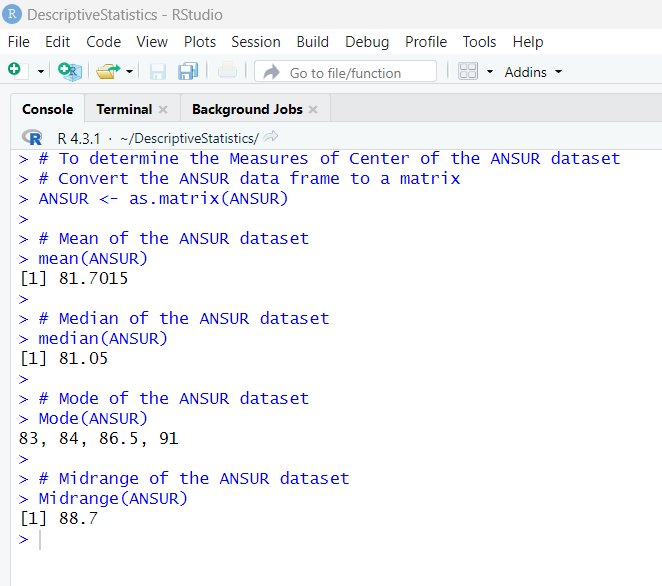
Statistical functions in R are used for statistical computations/analysis of a dataset.
Some statistical functions are already defined in R (these are built-in functions also known as system-defined functions)
For all other functions not built-in, we have to define them. These are known as user-defined functions.
As at today: 07/05/2023;
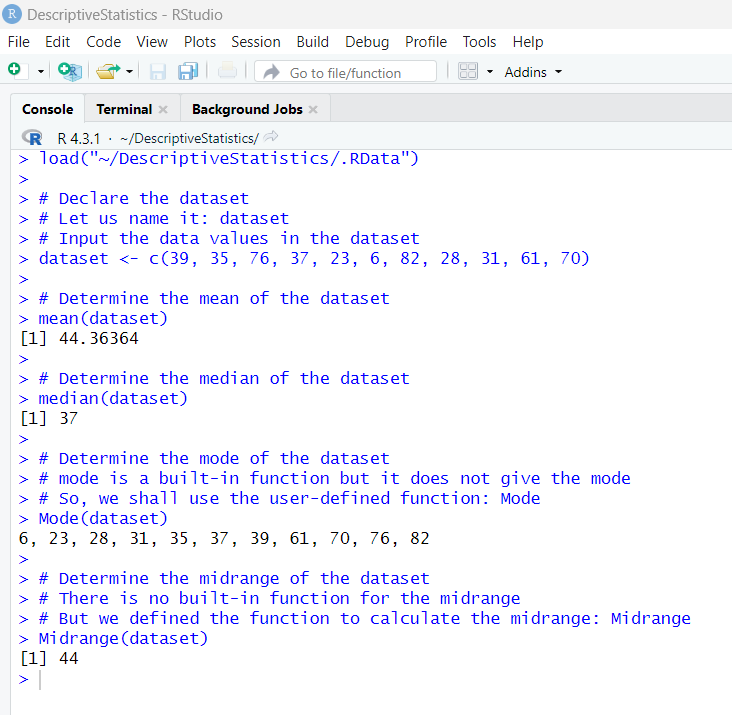
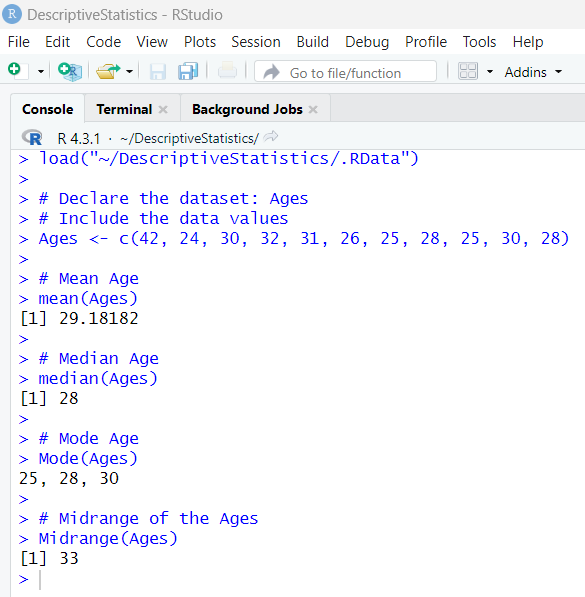
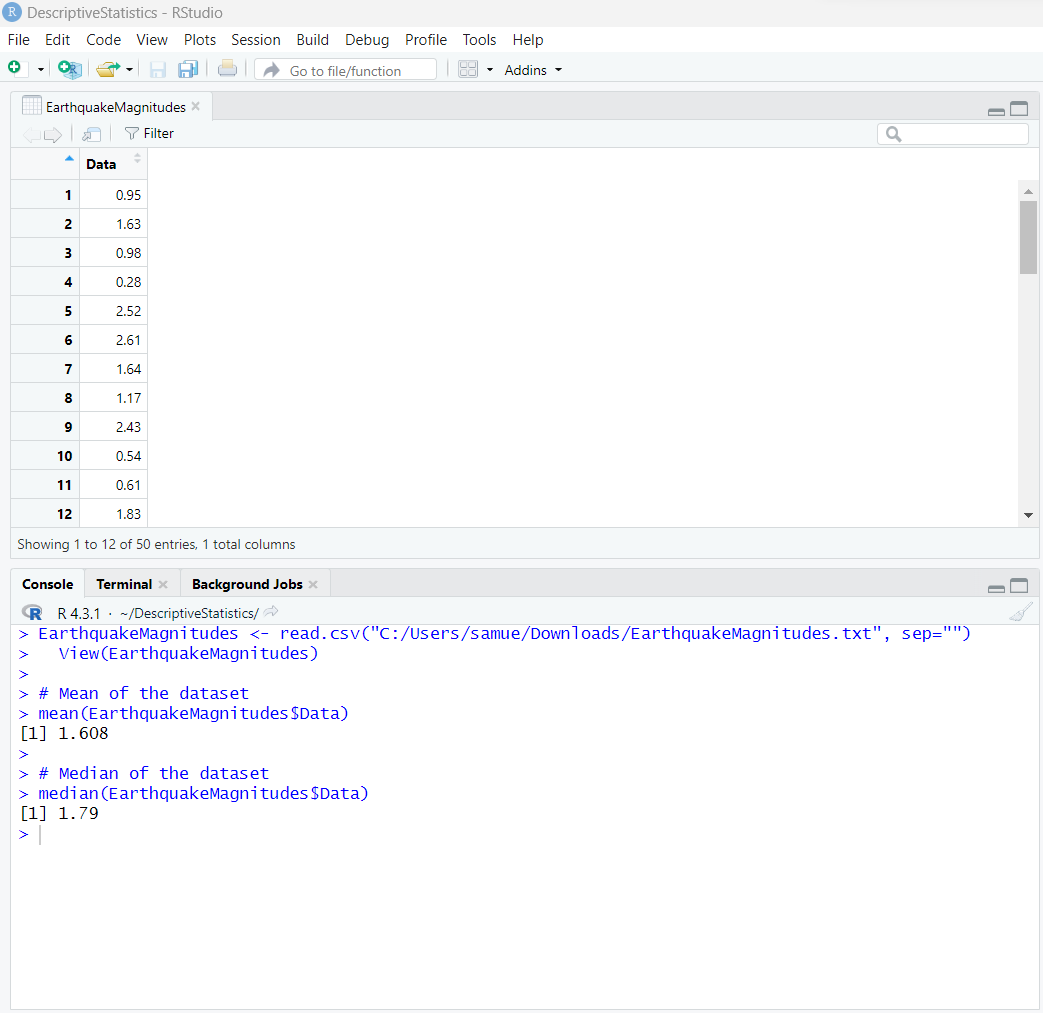
R programming language has these descriptive statistics represented by these built-in functions.
Let us review them.

This means that:
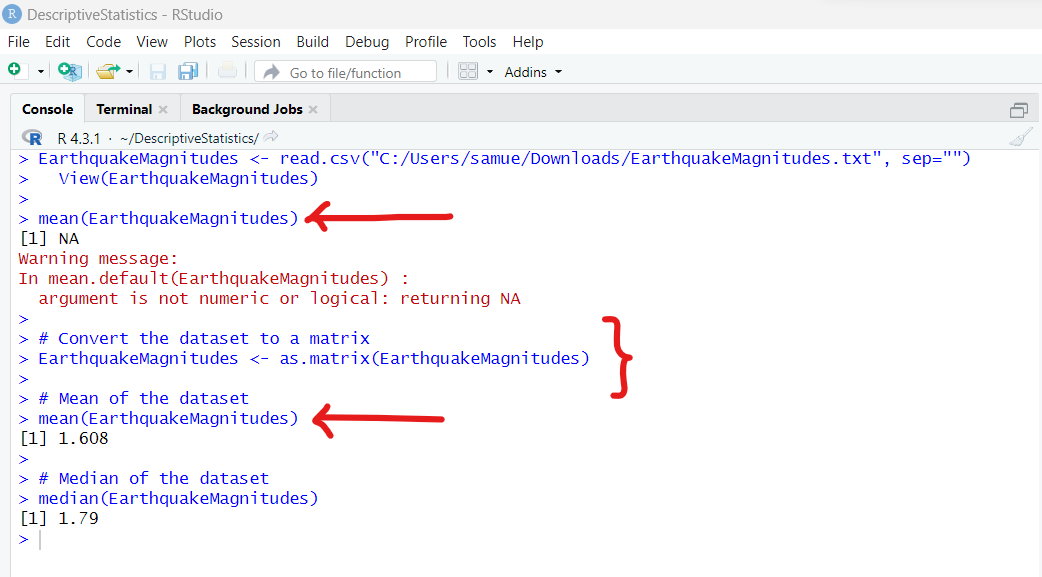
(1.) We cannot use the built-in function names as names for any user-defined variable or user-defined function.
(2.) We have to define our own functions (user-defined functions) for any function that is not built-in.
In that sense, we shall:
(a.) create a project in RStudio
(b.) define all those functions in the project
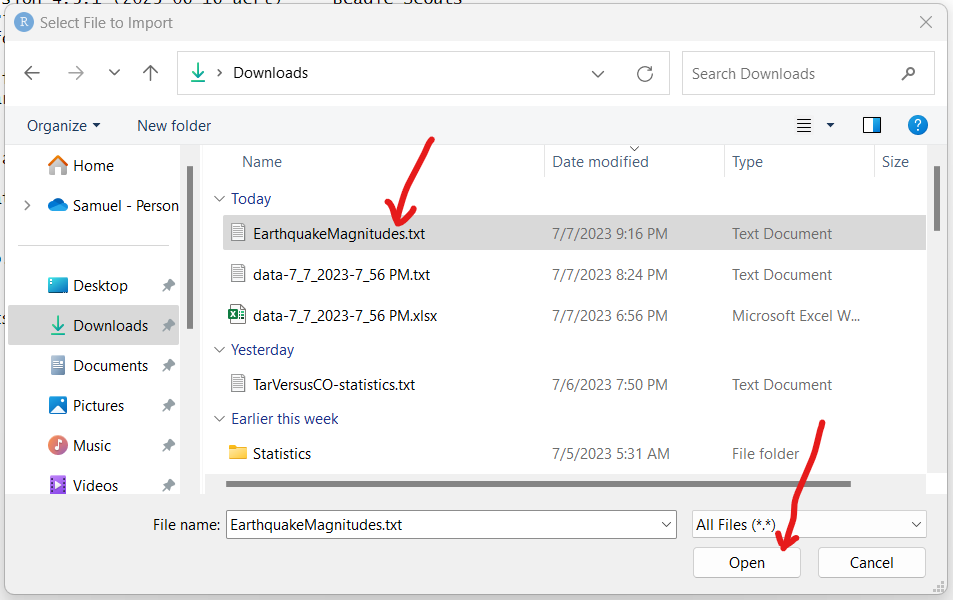
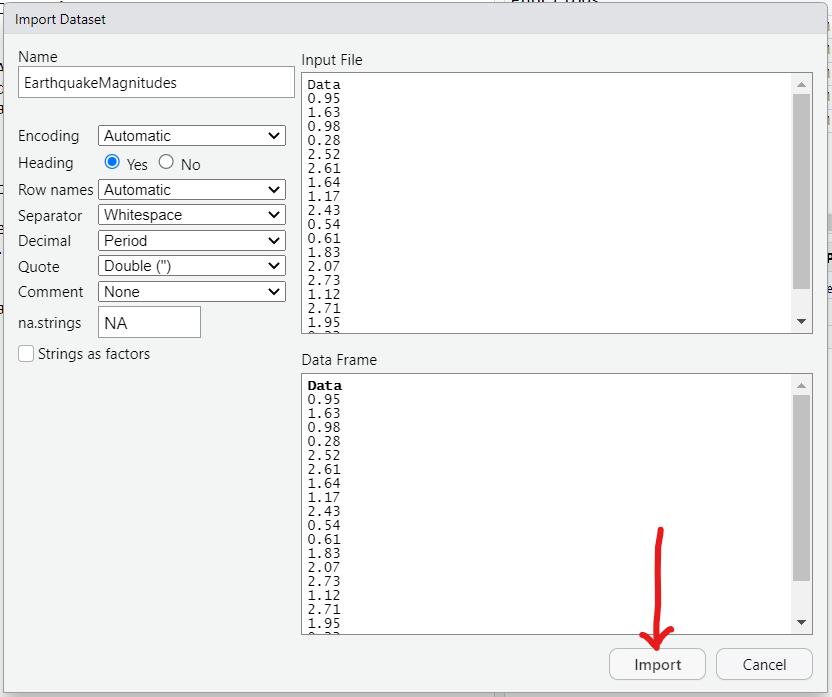
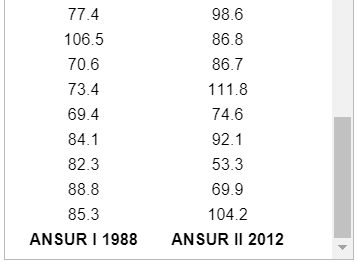
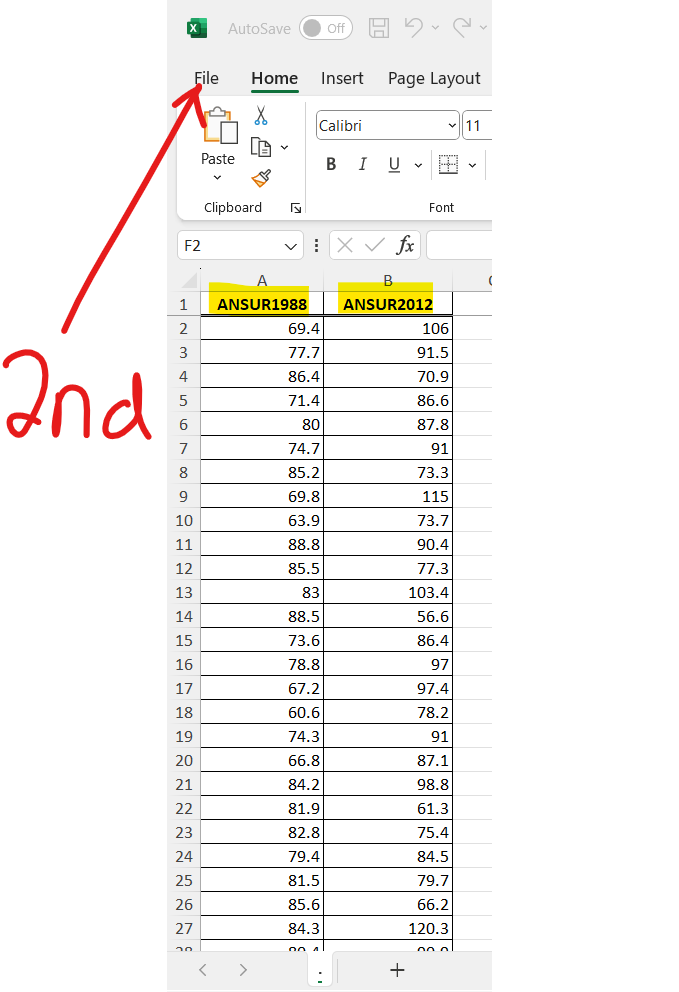
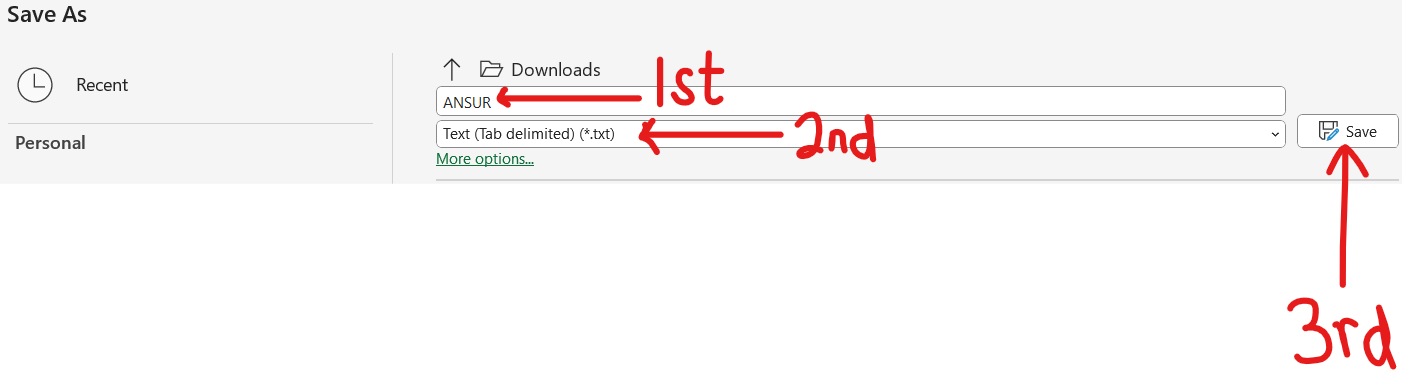
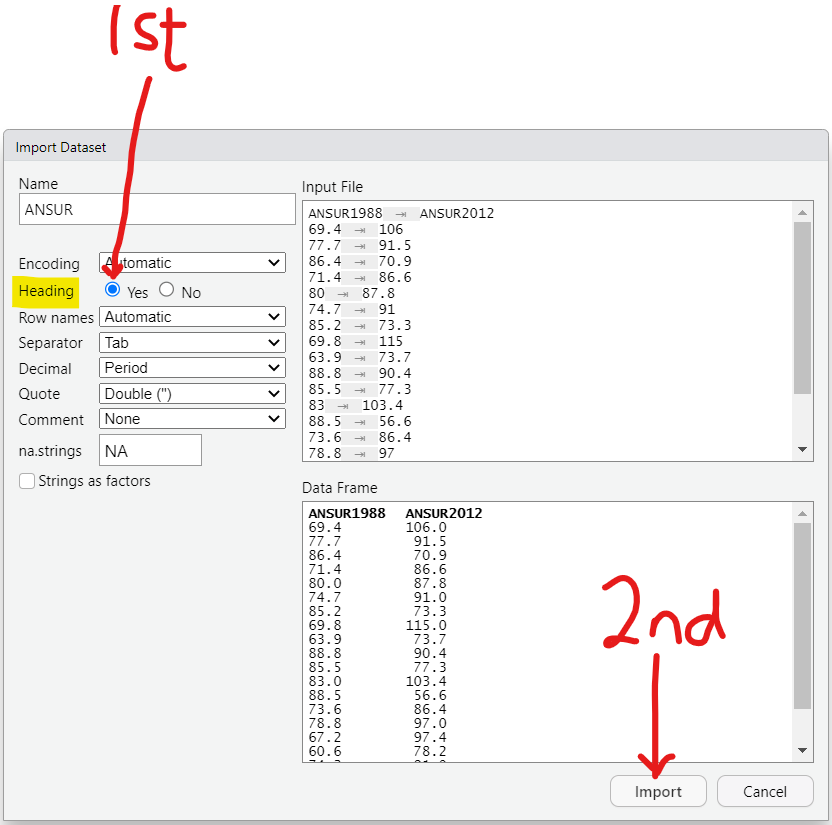
(c.) import any dataset we want into the project and use those functions in the dataset.

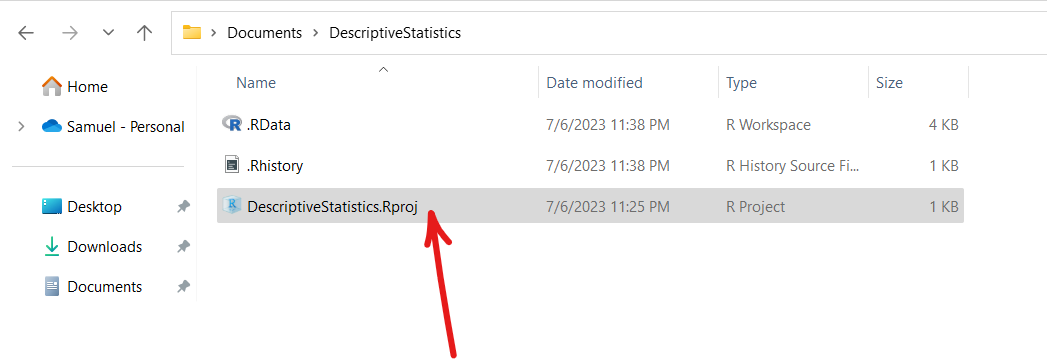
Create a Project in RStudio

(1.) Step 1: Open RStudio
Click: File → New Project...


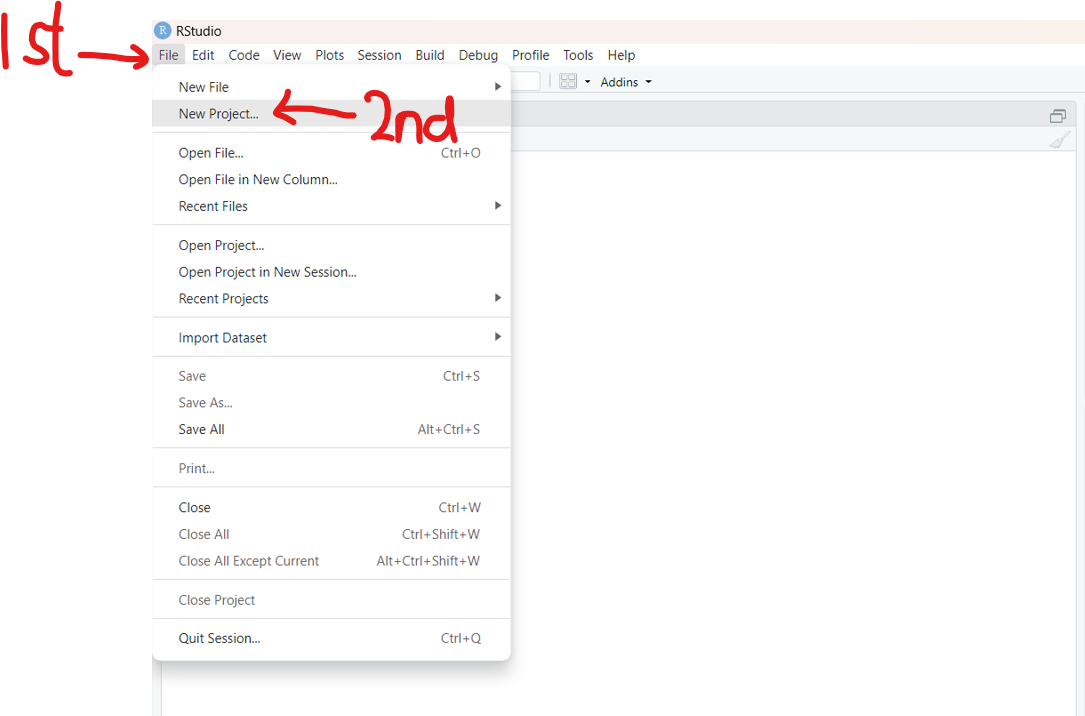
(2.) Step 2:


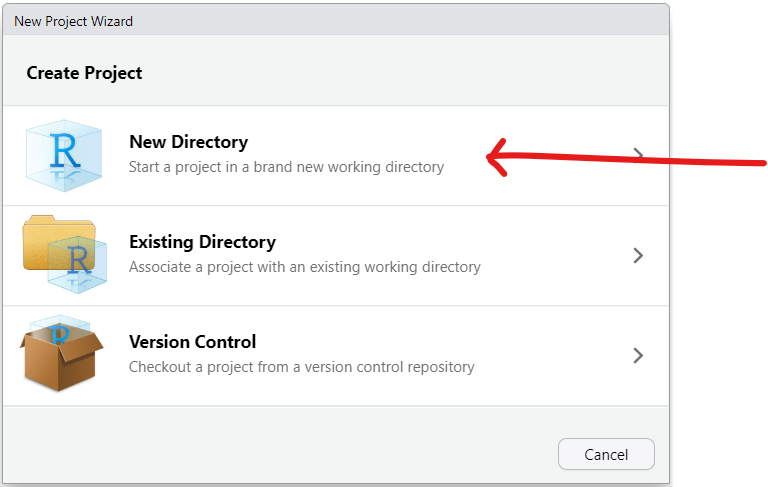
(3.) Step 3:


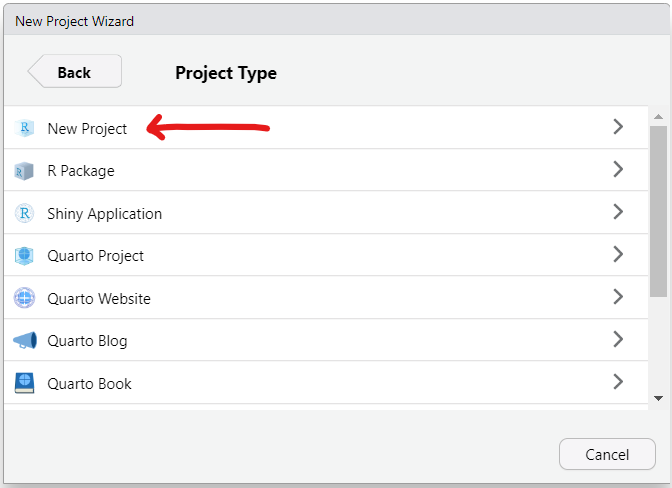
(4.) Step 4:


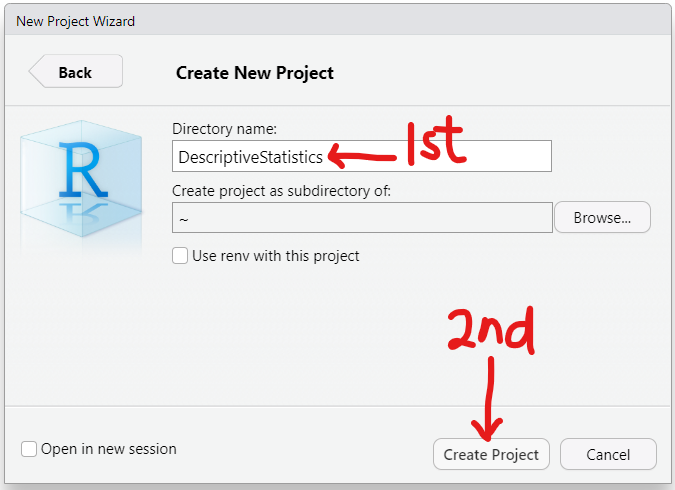
(5.) Step 5:


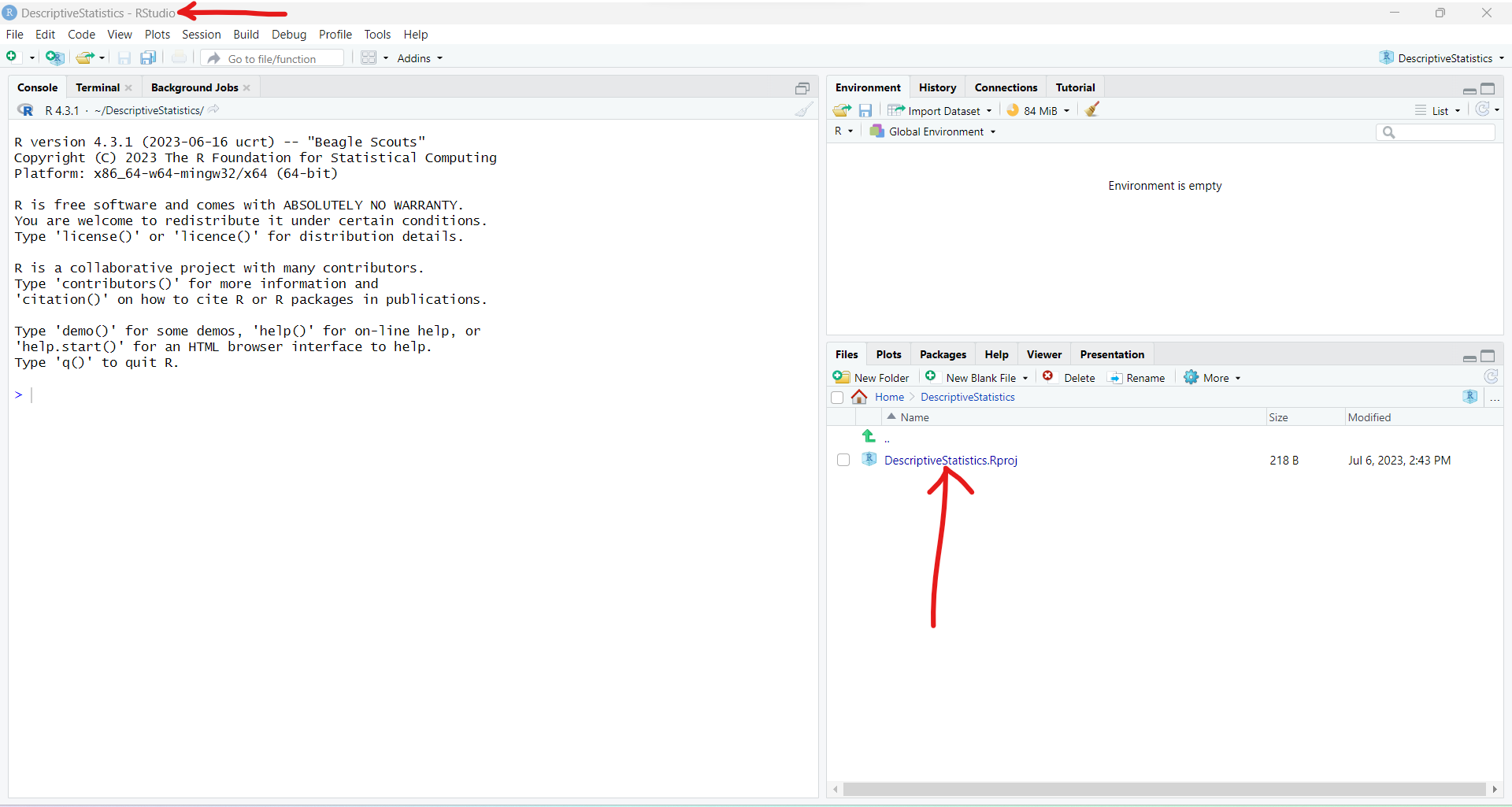
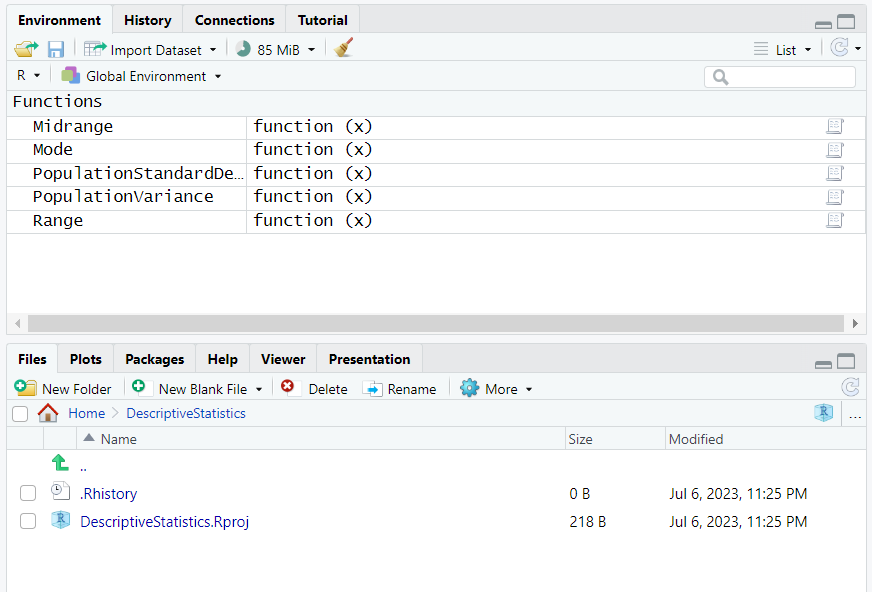
The project has been created.
By default, this project is located in the Documents folder of the Windows computer

(6.) Step 6:


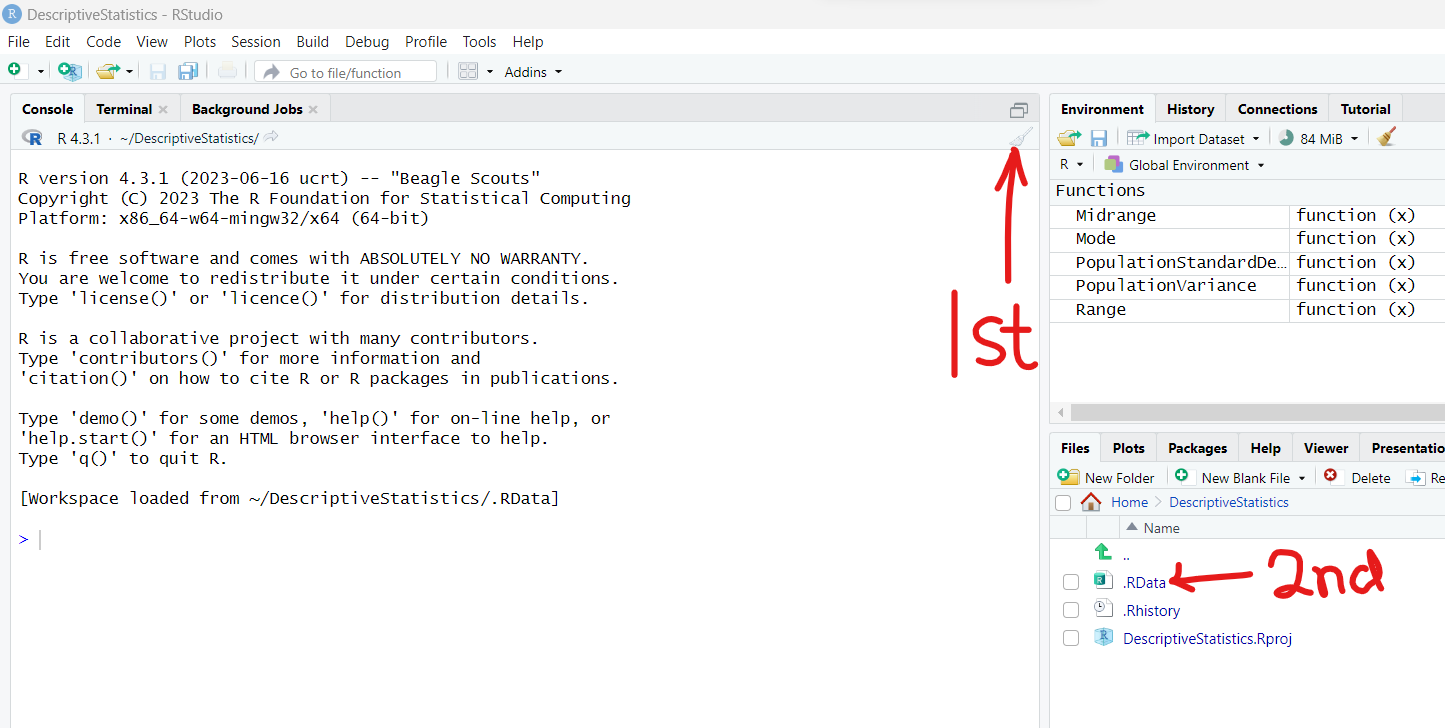
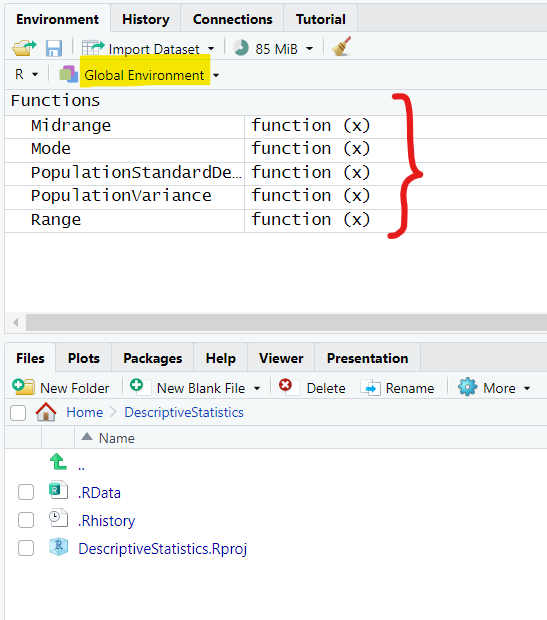
Let us go ahead and clear the default notes in the RStudio Console and let us write the remaining statistical functions.

User-Defined Functions

The syntax for writing a function is
functionName <– function(parameters)
{
    code/expression
}

Let us write functions for the rest of the descriptive statistics measures.

                    Measure of Center: Mode
                    # Function to calculate the mode of a dataset 
                    # It computes the mode for unimodal and multimodal data 
                    Mode <– function(x) 
                    { 
                        resultMode <– names(table(x))[table(x) == max(table(x))] 
                        cat(paste(resultMode, collapse = ", ")) 
                    }

                    # Call the function 
                    Mode(dataset)
                

                    Measure of Center: Midrange
                    # Function to calculate the midrange of a dataset 
                    Midrange <– function(x) 
                    { 
                        (min(x) + max(x)) / 2
                    }

                    # Call the function 
                    Midrange(dataset)
                

                    Measure of Spread: Range
                    # Function to calculate the range of a dataset 
                    Range <– function(x) 
                    { 
                        max(x) – min(x)
                    }

                    # Call the function 
                    Range(dataset)
                

                    Measure of Spread: Population Variance
                    # Function to calculate the population variance of a dataset 
                    PopulationVariance <– function(x) 
                    { 
                        var(x) * (length(x) – 1) / length(x)
                    }

                    # Call the function 
                    PopulationVariance(dataset)
                

                    Measure of Spread: Population Standard Deviation
                    # Function to calculate the population standard deviation of a dataset 
                    PopulationStandardDeviation <– function(x) 
                    { 
                        sd(x) * sqrt((length(x) – 1)/length(x))
                    }

                    # Call the function 
                    PopulationStandardDeviation(dataset)
                

Please NOTE:
(1.) For all the functions we have discussed so far: system-defined and user-defined functions, dataset is the raw data.

(2.) For Ungrouped Data: if we want to find the descriptive statistics of a specific column, we write the code as:
descriptiveStatistics(FileName$ColumnName)
where:
descriptiveStatistics is any measure of center, measure of spread, measure of position, or measure of shape
FileName is the name of the file
The dollar symbol, $ is the operator used to access the dataset by the column names.
ColumnName is the column that you want to determine the descriptive statistics.

(3.) For Ungrouped Data: if we want to find the descriptive statistics of the entire dataset (all the columns), we need to convert the dataset to a matrix using the code:
FileName <– as.matrix(FileName)
where:
as.matrix is the built-in function to convert a dataset to a matrix

(4.) For Grouped Data: there is no built-in function as at today: 07/07/2023
So, we shall write the function for the descriptive statistics and/or install library packages for it such as the actuar package (R package for Actuarial Science functions) among others.

Saving and Loading User-Defined Functions

After writing these functions, we need to save them as a workspace image.

(1.) This is what we have at the moment:
(a.)

(b.)

(2.) Step 2: Try to close the project


(3.) Save
It is saved as .RData file


(4.) Double-click the project, DescriptiveStatistics.Rproj to open it


(5.) Clear the Console window and Click the .RData file to load it in the Global Environment
(a.)

Load the .RData file into the Global Environment
(b.)

(c.) The user-defined functions are in the Global Environment
This implies that we can use them in the Console window for any dataset in that window, be it written or imported, provided they are seen there.
If we clear the Global Environment, then we will need to click the .RData file again to load it in the environment.


Let us begin to solve questions.
After each question, clear the Console window.

(1.) Listed below are the jersey numbers of 11 players randomly selected from the roster of a championship sports team.
39     35     76     37     23     6     82     28     31     61     70

Determine the:
(a.) mean
(b.) median
(c.) mode
(d.) midrange for the data
Type an integer or a decimal rounded to one decimal place as needed.

(e.) What do the results tell​ us?
(I.) The midrange gives the average​ (or typical) jersey​ number, while the mean and median give two different interpretations of the spread of possible jersey numbers.
(II.) The jersey numbers are nominal data and they do not measure or count​ anything, so the resulting statistics are meaningless.
(III.) The mean and median give two different interpretations of the average​ (or typical) jersey​ number, while the midrange shows the spread of possible jersey numbers.
(IV.) Since only 11 of the jersey numbers were in the​ sample, the statistics cannot give any meaningful results.

The sample size is 11.
It is not a lot. So, let us just type the code directly in RStudio.



(a.) Mean = 44.36364 ≈ 44.4
(b.) Median = 37
(c.) There is no mode because each value occurred one time.
(d.) Midrange = 44
(e.) The jersey numbers are nominal data and they do not measure or count​ anything, so the resulting statistics are meaningless.

(2.) Listed below are the ages of 11 players randomly selected from the roster of a championship sports team.



Find the:
(a.) mean
(b.) median
(c.) mode
(d.) midrange of the Ages
Type an integer or a decimal rounded to one decimal place as needed.

(e.) Determine how the resulting statistics are fundamentally different from those calculated from the jersey numbers of the same 11 players.

There are only 11 ages so let us just type it in the RStudio console



(a.) The mean age is: 29.18182 ≈ 29.2 years
(b.) The median age is: 28 years
(c.) The modes are: 25, 28, 30 years
(d.) The midrange is: 33 years
(e.) The jersey numbers are data at the nominal level of​ measurement, but the ages (in years) are data at the ratio level of​ measurement, so only the age statistics are meaningful.

(3.) Use the magnitudes​ (Richter scale) of the earthquakes listed in the data set below.



(A.) Find the mean of the data set.
(B.) Determine the median of the data set.
Round to three decimal places as needed.

(C.) Is the magnitude of an earthquake measuring 7.0 on the Richter scale an outlier​ (data value that is very far away from the​ others) when considered in the context of the sample data given in this data​ set? Explain.
I. No, because this value is not the maximum data value.
II. No, because this value is not very far away from all of the other data values.
III. Yes, because this value is very far away from all of the other data values.
IV. Yes, because this value is the maximum data value.

The sample size is a bit large. So, let us: export the data as an Excel file, save it as a Text file (.txt) and import it in RStudio.


(a.) Step 1:


(b.) Step 2:
There is no column name for the data. Let us insert a row and name it: Data
Then, we can name it with an appropriate name, and save it as a .txt file


(c.) Step 3:


(d.) Step 4:


(e.) Step 5:


(f.) Step 6:


(g.) Step 7:


(h.) Questions (A.) and (B.)
We have at least two approaches to solve the question.

1st Approach: Code Dataset by Column
File Name: EarthquakeMagnitudes.txt
Column Name: Data
We can go ahead and find the mean and the median.
The code to determine the mean is:

                        # Mean of the dataset 
                        mean(EarthquakeMagnitudes$Data)
                    

The code to determine the median is:

                        # Median of the dataset 
                        median(EarthquakeMagnitudes$Data)
                    

2nd Approach: Code Dataset
File Name: EarthquakeMagnitudes.txt
Please see the screenshot below: We need to convert the dataset to a matrix.
The code to convert the dataset to a matrix is:

EarthquakeMagnitudes <– as.matrix(EarthquakeMagnitudes)

Yes, we can use the same file name. I prefer to use the same file name for the converted file (matrix).
However, you may choose a new file name for the matrix.
If I still needed to do more work with the initial file "as is", then I will use a new file name.

The code to determine the mean is:

                        # Mean of the dataset 
                        mean(EarthquakeMagnitudes)
                    

The code to determine the median is:

                        # Median of the dataset 
                        median(EarthquakeMagnitudes)
                    

mean = 1.608
median = 1.79

(C.) The dataset: EarthquakeMagnitudes has values from 0.something to 2.something
7.0 is far from these decimals. Hence, it is an outlier when compared to all other data values.
Yes, because this value is very far away from all of the other data values.

(4.) ANSUR is an abbreviation of​ "anthropometric survey."
Use the accompanying sample of weights​ (kg) of the males from the data set ​"​ANSUR I 1988," which were measured from U.S. army personnel in 1988.
Use the accompanying sample of weights​ (kg) of the males from the data set ​"​ANSUR II 2012," which were measured from U.S. army personnel in 2012.
Use software or a calculator to find the:
(a.) means.
(b.) medians.
Type an integer or decimal rounded to two decimal places as​ needed.







(c.) Does it appear that males have become​ heavier?

(d.) Determine the measures of center of the entire dataset.

(a.)

Mean of the ANSUR I 1988 dataset = 78.843 ≈ 78.84kg
Mean of the ANSUR II 2012 dataset = 84.56kg

(b.)

Median of the ANSUR I 1988 dataset = 78.6kg
Median of the ANSUR II 2012 dataset = 84.1kg

(c.) Does it appear that males have become heavier?
Yes, because the mean increased from 1988 to 2012 and the median increased from 1988 to 2012.

(d.)

Mean of the ANSUR dataset = 81.7015kg
Median of the ANSUR dataset = 81.05kg
Mode of the ANSUR dataset = 83kg, 84kg, 86.5kg, 91kg
Midrange of the ANSUR dataset = 88.7kg