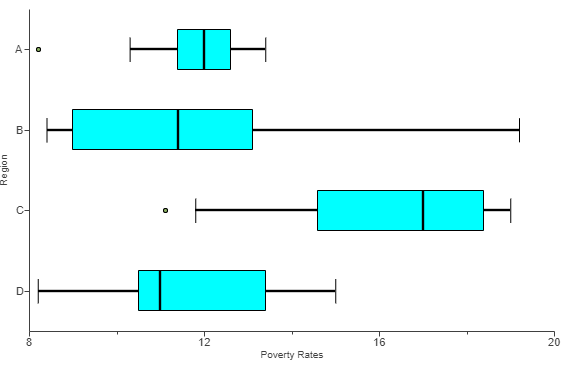
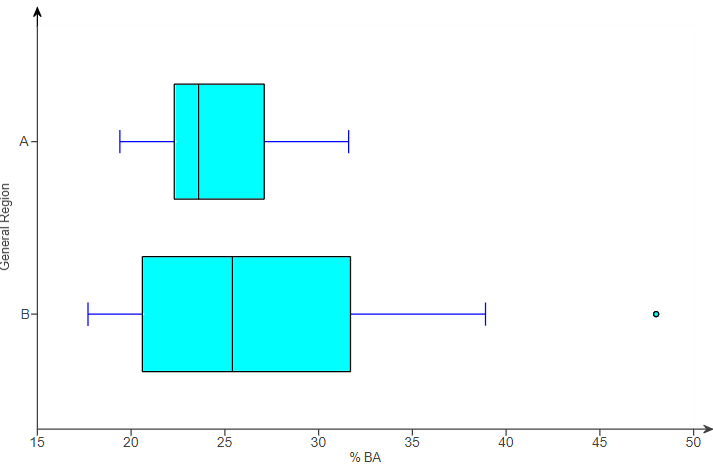
(9.) The boxplot displayed shows the average ticket price for four professional sports leagues.
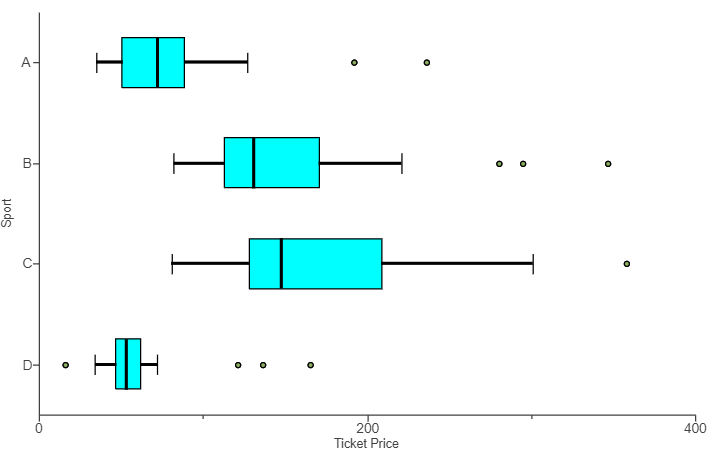
(a.) Which sport has the most expensive ticket prices?
(b.) Which sport has the least expensive ticket prices?
(c.) Compare the ticket prices for Sport A and Sport B.
In your comparison, compare the price of a typical ticket, the amount of variation in ticket prices, and the presence of any outliers in the data.
(a.) The sport with the most expensive ticket prices is Sport C because it has the greatest maximum ticket price.
(b.) The sport with the most expensive ticket prices is Sport D because it has the least minimum ticket price.
(c.) A typical ticket for Sport A is less expensive than a typical ticket for Sport B, since Sport A has a lower median than Sport B.
Sport B has more variability in ticket prices, as shown by a higher IQR (the length of the box...without the whiskers).
Sport A has potential outliers representing unusually high-priced tickets.
Sport B has potential outliers representing unusually high-priced tickets.

(a.) Which sport has the most expensive ticket prices?
(b.) Which sport has the least expensive ticket prices?
(c.) Compare the ticket prices for Sport A and Sport B.
In your comparison, compare the price of a typical ticket, the amount of variation in ticket prices, and the presence of any outliers in the data.
(a.) The sport with the most expensive ticket prices is Sport C because it has the greatest maximum ticket price.
(b.) The sport with the most expensive ticket prices is Sport D because it has the least minimum ticket price.
(c.) A typical ticket for Sport A is less expensive than a typical ticket for Sport B, since Sport A has a lower median than Sport B.
Sport B has more variability in ticket prices, as shown by a higher IQR (the length of the box...without the whiskers).
Sport A has potential outliers representing unusually high-priced tickets.
Sport B has potential outliers representing unusually high-priced tickets.
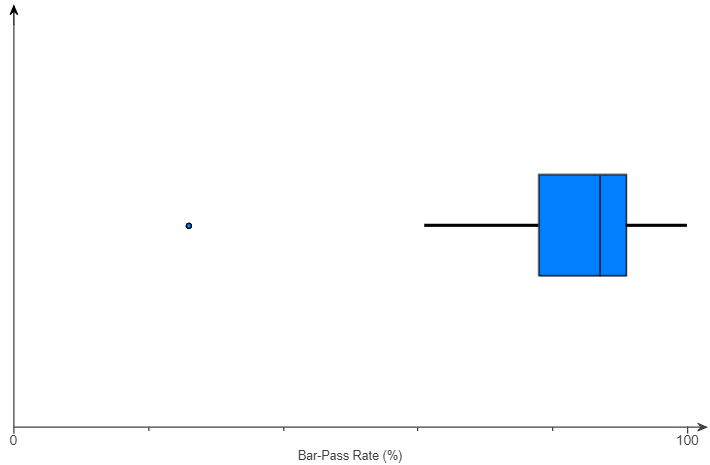
(10.) Determine the five-number summary for the dataset
$ 70\hspace{4em}71\hspace{4em}71\hspace{4em}71\hspace{4em}72 \\[3ex] 72\hspace{4em}74\hspace{4em}74\hspace{4em}76\hspace{4em}77 \\[3ex] 78\hspace{4em}78\hspace{4em}79\hspace{4em}79\hspace{4em}79 \\[3ex] $
The data is already arranged in ascending order.
$ n = 15 \\[3ex] Min = 70 \\[3ex] xth\;\;position = \dfrac{1}{4} * 15 = 3.75 \approx 4th\;\;position = 71 \\[5ex] Q_1 = 71 \\[3ex] xth\;\;position = \dfrac{2}{4} * 15 = 7.5 \approx 8th\;\;position = 74 \\[5ex] Q_2 = 74 \\[3ex] xth\;\;position = \dfrac{3}{4} * 15 = 11.25 \approx 12th\;\;position = 78 \\[5ex] Q_3 = 78 \\[3ex] Max = 79 \\[3ex] $ The five-number summary: 70, 71, 74, 78, 79
$ 70\hspace{4em}71\hspace{4em}71\hspace{4em}71\hspace{4em}72 \\[3ex] 72\hspace{4em}74\hspace{4em}74\hspace{4em}76\hspace{4em}77 \\[3ex] 78\hspace{4em}78\hspace{4em}79\hspace{4em}79\hspace{4em}79 \\[3ex] $
The data is already arranged in ascending order.
$ n = 15 \\[3ex] Min = 70 \\[3ex] xth\;\;position = \dfrac{1}{4} * 15 = 3.75 \approx 4th\;\;position = 71 \\[5ex] Q_1 = 71 \\[3ex] xth\;\;position = \dfrac{2}{4} * 15 = 7.5 \approx 8th\;\;position = 74 \\[5ex] Q_2 = 74 \\[3ex] xth\;\;position = \dfrac{3}{4} * 15 = 11.25 \approx 12th\;\;position = 78 \\[5ex] Q_3 = 78 \\[3ex] Max = 79 \\[3ex] $ The five-number summary: 70, 71, 74, 78, 79