Descriptive Statistics


I greet you this day,

First: Read the Stories (Yes, I tell stories too. ☺)
The stories will introduce you to the topic, while making you smile/laugh at the same time.
Second: Review the Notes/eText.
Third: View the Videos/Multimedia Resources.
Fourth: Solve the questions/solved examples.
Fifth: Check your solutions with my thoroughly-explained solved examples.

I wrote some of the codes for the calculators using JavaScript, a client-side scripting language. In addition, I used the AJAX Javascript library. Please use the latest Internet browsers. The calculators should work.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome. Should you need to contact me, please use the form at the bottom of the page. Thank you for visiting.

Samuel Chukwuemeka (Samdom For Peace) B.Eng., A.A.T, M.Ed., M.S

Story on the Measures of Center

It was a Saturday
A family of the Dad, Mom, Daughter, Son
The two children are in middle school.
The Dad and Mom were reviewing the notes of their children
The children were reading books.
All of them were in the living room at home.


Dad: Elijah
Son: Yes, Dad
Dad: Esther
Daughter: Yes, Dad
Dad: A philanthropist wanted to buy shoes for the motherless and fatherless children at an orphanage.
There were $300$ children at the orphanage.
He arrived at the orphanage and asked for a shoe size.
What shoe size should the director recommend?
Son: He asked for just a shoe size...
Rather than shoe sizes?
Dad: Yes. Do you not think it is cumbersome to ask for the shoe sizes of $300$ children?
Son: But, if he really wanted to help, why would he not help "all" of them?
Typically, all of them would not have the same shoe size.
So, why not just make everyone happy by providing each one with the shoe that fits him/her?
Dad: I understand.
But, let's assume he just wanted a shoe size.
What shoe size should the director give?
Son: But, Dad; why would he want to do that?
Dad: Answering questions with questions...typical of a Nigerian
Just answer my question or say you do not know the answer.
Rather than answering it with a question
Son: I have your gene, Dad ☺
Dad: Whatever...
But, I want you to think about it... while I ask your sister
Esther, what shoe size would the director recommend?
Daughter: I think Elijah made a point.
Why would the philanthropist choose to buy shoes of only one size?
One size certainly does not fit all.

Mom: Listen my children.
Your Dad is indirectly asking you about what you learned in school last week.
He wants you to see the connection/application of what you learned.
Daughter: Okay, Mom. I get it.
The director can measure the shoe sizes of the $300$ children.
Find the sum.
And divide by $300$
That is known as the Mean or Average
Dad: Correct! Proud of you, Daddy's girl! ☺
Son: The second way would be the arrange all those measured shoe sizes in order ...
Preferably in ascending order
Because it is an even sample size, there would be two sizes in the middle.
So, find the average of those two sizes.
That measure is the Median
Mom: Perfect! Mummy's boy! ☺
But, why would you arrange the sizes in ascending order?
What about descending order?
Would it not give the same result?
Daughter: Mom, guess what? ☺
That was the same question Elijah asked Mr. C in the class ☺
Mom: What did he say?
Son: He said that it is normal to start from the kindergarten up to the $12^{th}$ grade...
Rather than from the $12^{th}$ grade to the kindergarten
Dad: Wow, that is an "okay" answer. Is that the only reason?
Daughter: He also said that when we study the Quartiles, we must have to arrange it in ascending order.
So, it is better to just learn to arrange the data in ascending order.
Dad: That is correct.
What other ways do we have?
Daughter: The director can find the most popular shoe size
Dad: What do you mean by "most popular"?
Daughter: By "most popular", I mean the shoe size that most of the children wear
Dad: Okay, but I am looking for a term... a statistics term...
Son: It means the shoe size with the highest frequency.
Dad: and the measure is called the ...
Daughter: Mode
Dad: Wow, my children are wonderful! Thank GOD!
Mom: Our children...
Dad: Yes, GOD gave us intelligent children.
Mom: What is the remaining measure of center?
Son: It's my turn this time.
The fourth measure is the Midrange
The director can take the average of the minimum shoe size and the maximum shoe size.
Mom and Dad: That is correct!

Dad: These are called the Measures of Center
Mom: or the Measures of Central Tendency
Dad: because they tend towards the "center" of the data set
Mom: and the center is seen as a representative of the whole.
Dad: The mean or average is the most used.
Although each of these measure has it's advantages and disadvantages
Mom: The midrange is also an average.
Dad: And if the sample size is an even number, the median is also an average.

Daughter: Thank You, Dad! Thank You, Mom!
Son: Thank You, Mom! Thank You, Dad!
Dad and Mom: You are most welcome!!!

Objectives

Students will:
(1.) Discuss descriptive statistics.
(2.) Explain the measures of center.
(3.) Compute the measures of central tendency of data by formula.
(4.) Compute the measures of central tendency of data by technology.
(5.) Compute the measures of central tendency of data by formula.
(6.) Explain the measures of spread.
(7.) Compute the measures of variation of data by formula.
(8.) Compute the measures of dispersion of data by technology.
(9.) Explain the measures of position.
(10.) Compute the measures of location of data by formula.
(11.) Compute the measures of position of data by technology.
(12.) Define z-scores.
(13.) Interpret z-scores
(14.) Convert a data value to a quantile.
(15.) Convert a quantile to a data value.
(16.) Determine the five-number summary of a data set.
(17.) Construct a boxplot for a data set.
(18.) Determine outliers using fences.
(19.) Explain the shape of the distribution of data.
(20.) Solve applied problems on descriptive statistics.



Definitions

Descriptive Statistics is the science that deals with the organization and presentation of the collected data.

Symbols

Measures of Center

The Measures of Center is also known as the Measures of Central Tendency
They are called the measures of central tendency because they tend towards the center of the data set.
Most times, the center of the data can be seen as a representative of the entire sample data or population data.

The measures of center are:

(1.) Mean of Average, $\bar{x}$

(2.) Median, $\tilde{x}$

(3.) Mode, $\widehat{x}$

(4.) Midrange, $x_{MR}$

Mean or Average

The Mean is commonly referred to as the Arithmetic Mean.
It is another term for the arithmatic average. It can be thought of as the balancing point of a distribution of data.
The mean of a collection of data is located at the​ "balancing point" of a distribution of data.
We do have other types of mean: Geometric Mean, Quadratic Mean, and Harmonic Mean
We can also trim the dataset to determine the trimmed mean.

The Arithmetic Mean is the measure of center found by adding the data values of the variable and dividing the sum by the count/total number of the data values.

Why Arithmetic Mean?: Have you heard of these statements?

(1.) The average miles per gallon of the $2015$ Hyundai Santa Fe in the highway is $36\:mpg$

(2.) Mr. C uses the weighted average method for determining the final grade of his students' work.

(3.) The Consumer Price Index ($CPI$) is a measure of the average change in price over time in a fixed market basket of goods and services bought by customers for day-to-day living.

(4.) To be admitted into the graduate program at a certain university, you must have at least an undergraduate cumulative grade point average ($CGPA$) of $3.00$

(5.) According to the Bureau of Labor Statistics ($BLS$), the average expenditures in $2014$ was $\$53,495$, a $4.7$ percent increase from $2013$ spending level.

(6.) What was your grade point average ($GPA$) last semester?

Advantages of the Mean

(1.) The mean of a data set uses every data value.

(2.) Sample means drawn from the same population tend to have less variation when compared to the other measures of center.

(3.) The mean is the most appropriate measure of center for symmetric (normal) distributions.

mean
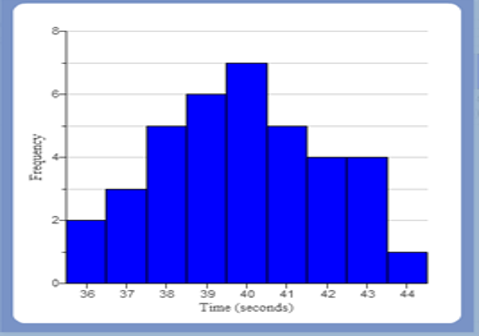
Normal (Symmetric) Distribution

(4.) The mean of a population can be estimated to be the sample means of the samples drawn from that population.
This implies that: $ \mu = \bar{x}_{\bar{x}} $

Disadvantages of the Mean

(1.) The value of the mean can substantially change due to the presence of an outlier in the data set. In this regard, we say that the mean is not resistant.
An outlier is an extreme data value - that is either too low or too high relative to the other data values.

(2.) The mean is not an appropriate measure of center for skewed distributions.

Round-Off Rules for the Mean

Except otherwise stated, it is suggested to round the final answer (not intermediate calculations) of the mean to one more decimal place than the original set of data values.
Do not round intermediate calculations.
If you must round intermediate calculations, round to a reasonable number of decimal places (at least three) more than the number of decimal places required for the answer.

Median

The Median is also the Middle Quartile or the 2nd Quartile or the 50th Percentile.
It is the middle value of a data value when the data set is sorted in ascending or descending order. However, it is better to sort the data in ascending order rather than descending order.
Sorting in ascending order (ordering from least to greatest) is highly recommended.

Student: Why is the ascending order preferred over descending order?
The answer would still be the same either way. Is that right?

Teacher: Yes, that is correct.
However, when we discuss Quartiles - a measure of location, we shall have to sort in ascending order.
Besides, one normally begins from the kindergarten up to the $12^{th}$ grade, and not the other way around.

The median is the value that would be right in the middle if you were to sort the data from smallest to largest (ascending order).
About​ 50% of the observations are below it and about​ 50% of the observations are above it.
For an odd sample size (the sample size is an odd number), there is only one middle value. That value is the median.

For an even sample size (the sample size is an even number), there are two middle values. The median is the average of those two middle values.

Why Median?: Have you heard of these statements?

(1.) The median household income for a $6-person$ family in the State of Arizona during $2016$ is $\$51,590.00$ - Arizona State Median Income for Fiscal Year 2016 - The LIHEAP Clearinghouse
What does this mean?
This means that of all $6-person$ families in the State of Arizona, $\$51,590.00$ divides the lower half of incomes from the upper half of the incomes.

(2.) The median home price for the homes sold in the San Francisco Bay Area in March $2017$ was $\$709,000.00$: Bay Area Median Home Price Approaches All-Time High - CBS San Francisco Wow!

(3.) The median age at first marriage by men in the United States for $2003$ is $27.1$ years - Estimated Median Age at First Marriage, by Sex - U.S Bureau of the Census

Advantages of the Median

(1.) The median is resistant to outliers.
It is not affected by extremely low or extremely high data values.

(2.) The median is the most appropriate measure of center for skewed distributions.
The mean is not often used for skewed distributions because skew affects the mean more than it affects the median.

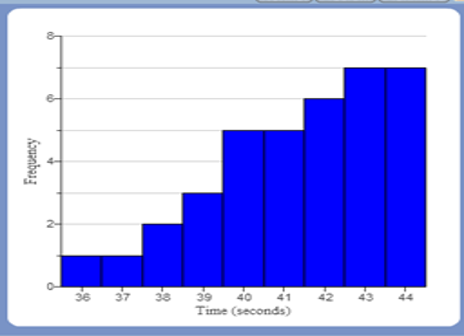median 1
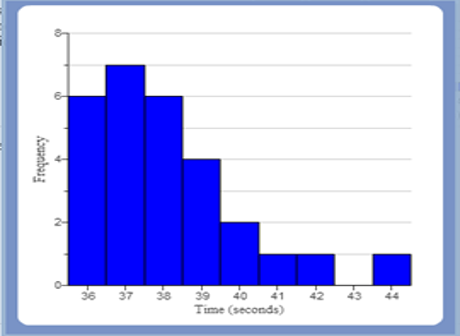Skewed Distribution (Skewed Left) 		median 2
Skewed Distribution (Skewed Right)


Disadvantages of the Median

(1.) The median does not use every data value in the data set.

(2.) Computing the median of a grouped data algebraically is a bit cumbersome.

Round-Off Rules for the Median

Except otherwise stated, it is suggested to round the final answer (not intermediate calculations) of the mean to one more decimal place than the original set of data values.
Do not round intermediate calculations.
If you must round intermediate calculations, round to a reasonable number of decimal places (at least three) more than the number of decimal places required for the answer.



Mode

The Mode is the data value that occurs most frequently in a data set.
It can also be defined as the data value with the highest frequency.

Why Mode?: Have you heard of these statements?

(1.) Louisville Quarterback, Lamar Jackson won the $2016$ Heisman Trophy award because he received the most first-place votes - The New York Times

(2.) The modal age of the population of New Zealand from $1970 - 2010$ shows a similar pattern for males and females from $1970 - 1989$. Then, the pattern for males and females diverge - National Population Estimates: September 2010 Quarter - Government of New Zealand

Advantages of the Mode

(1.) The mode is resistant to outliers. It is not affected by extremely low or extremely high data values.

(2.) The mode is the most appropriate measure of center for qualitative data.

(3.) The mode is the most appropriate measure of center for the nominal level of measurement of a variable.

Disadvantages of the Mode

(1.) The mode does not use every data value in the data set.

(2.) A data set can have two modes (bimodal data set), more than two modes (multimodal data set), or no mode at all. In such cases, the mode is not a good measure of center.

(3.) Computing the mode of a grouped data algebraically is a bit cumbersome.

Round-Off Rules for the Mode

Except otherwise stated, it is suggested to leave the mode as is

Midrange

The Midrange is the average of the minimum and maximum values of a data set.
It is also known as Midextreme.

Why Midrange?: Have you heard of these statements?

(1.) Let us bring it to Algebra. Do you remember how to calculate the midpoint of two points? What is the formula?

$ For\:\:Point\:1\:(x_1, y-1) \:\:and\:\: Point\:2\:(x_2, y_2) \\[3ex] Midpoint\:\:Formula = \left(\dfrac{x_1 + y_1}{2}, \dfrac{x_2 + y_2}{2}\right) \\[5ex] $ (2.) What is a midrange computer system?

(3.) List some middle range watches. Give reasons for your answer.

Advantages of the Midrange

(1.) The midrange is very easy to compute.

(2.) The midrange is the most appropriate measure of center for uniform distributions.

Disadvantages of the Midrange

(1.) The midrange does not use every data value in the data set. It only uses two values - the minimum and maximum values.

(2.) The midrange is not resistant to outliers. It is extremely affected by it.

Round-Off Rules for the Median

Except otherwise stated, it is suggested to round the final answer (not intermediate calculations) of the mean to one more decimal place than the original set of data values.
Do not round intermediate calculations.
If you must round intermediate calculations, round to a reasonable number of decimal places (at least three) more than the number of decimal places required for the answer.

Formulas: Measures of Central Tendency

Raw Data and Ungrouped Data

$ \underline{Sample\:\:Mean} \\[3ex] (1.)\:\: \bar{x} = \dfrac{\Sigma x}{n} \\[5ex] (2.)\:\: n = \Sigma f \\[3ex] (3.)\:\: \bar{x} = \dfrac{\Sigma fx}{\Sigma f} \\[5ex] \underline{Given\:\:an\:\:Assumed\:\:Mean} \\[3ex] (4.)\:\: D = x - AM \\[3ex] (5.)\:\: \bar{x} = AM + \dfrac{\Sigma D}{n} \\[5ex] (6.)\:\: \bar{x} = AM + \dfrac{\Sigma fD}{\Sigma f} \\[7ex] \underline{Population\:\:Mean} \\[3ex] (7.)\:\: \mu = \dfrac{\Sigma x}{N} \\[5ex] (8.)\:\: N = \Sigma f \\[3ex] \underline{Given\:\:an\:\:Assumed\:\:Mean} \\[3ex] (9.)\:\: D = x - AM \\[3ex] (10.)\:\: \mu = AM + \dfrac{\Sigma D}{N} \\[5ex] (11.)\:\: \mu = AM + \dfrac{\Sigma fD}{\Sigma f} \\[7ex] \underline{Median} \\[3ex] (12.)\:\: \tilde{x} = \left(\dfrac{\Sigma f + 1}{2}\right)th \:\:for\:\:sorted\:\:odd\:\:sample\:\:size \\[5ex] (13.)\:\: \tilde{x} = \left(\dfrac{\Sigma f}{2}\right)th \:\:for\:\:sorted\:\:even\:\:sample\:\:size \\[7ex] \underline{Mode} \\[3ex] (14.)\:\: Mode = x-value(s) \:\;with\:\:highest\:\:frequency \\[5ex] \underline{Midrange} \\[3ex] (15.)\:\: x_{MR} = \dfrac{min + max}{2} \\[5ex] \underline{Geometric\;\;Mean} \\[3ex] (16.)\;\; GM = \sqrt[n]{\prod\limits_{x=1}^n x} $



Grouped Data

$ \underline{Class\:\:Midpoint} \\[3ex] (1.)\:\: x_{mid} = \dfrac{LCL + UCL}{2} \\[7ex] Equal\:\:Class\:\:Intervals\:(Same\:\:Class\:\:Size) \\[3ex] \underline{Mean} \\[3ex] (2.)\:\: \bar{x} = \dfrac{\Sigma fx_{mid}}{\Sigma f} \\[7ex] Equal\:\:Class\:\:Intervals\:(Same\:\:Class\:\:Size) \\[3ex] \underline{Given\:\:an\:\:Assumed\:\:Mean} \\[3ex] (3.)\:\: D = x_{mid} - AM \\[3ex] (4.)\:\: \bar{x} = AM + \dfrac{\Sigma fD}{\Sigma f} \\[7ex] \underline{Median} \\[3ex] (5.)\:\: \tilde{x} = LCB_{med} + \dfrac{CW}{f_{med}} * \left[\left(\dfrac{\Sigma f}{2}\right) - CF_{bmed}\right] \\[7ex] \underline{Mode} \\[3ex] (6.)\:\: \widehat{x} = LCB_{mod} + CW * \left[\dfrac{f_{mod} - f_{bmod}}{(f_{mod} - f_{bmod}) + (f_{mod} - f_{amod})}\right] $



Measures of Spread

The Measures of Spread is also known as the Measures of Variation or Measures of Variability
They are called the measures of spread because they move away from the center of the data set.

The measures of spread are:

(1.) Range, R

(2.) Variance, σ²

(3.) Standard Deviation, σ

(4.) Interquartile Range, IQR

Range

The Range is the difference between the maximum value and the minimum value of a dataset.

Variance

The Variance is the square of the standard deviation.

Advantages of the Variance

(1.) The standard deviation is preferred when the data is symmetric.

Standard Deviation

The Standard Deviation is a number that measures how far away the typical observation is from the mean.
It is the measure that tells us how far the data values are from the mean.
It is the square root of the average of the squared deviations from the mean.
In other words, it is the square root of the variance.
For most​ distributions, a majority of observations are within one standard deviation of the mean value.
If all the values of a dataset are the same, the standard deviation of that dataset is zero.
The standard deviation cannot be negative because it is the square root of the variance, which is a nonnegative value.
In the calculation of the standard deviation, all differences from the mean are​ squared, making all distances positive values.
For most​ applications, the standard deviation is preferred over the​ variance because the units for the variance are always squared. Measuring spread distance with the variance implies that the units for measuring spread are different from the units for measuring​ center, which is not true.

Advantages of the Standard Deviation

(1.) The standard deviation is preferred when the data is symmetric.

Interquartile Range

The Interquartile Range of a dataset is the difference between the upper quartile and the lower quartile of the dataset.
It tells us how much space the middle 50% of the data occupy.

Advantages of the Interquartile Range

(1.) The interquartile range is preferred when the data is strongly skewed, or has outliers.



Formulas: Measures of Dispersion

Raw Data and Ungrouped Data

$ \underline{Range} \\[3ex] (1.)\:\: Range = max - min \\[3ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (2.)\;\; D = x - AM \\[5ex] \underline{Sample\:\:Variance} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (3.)\:\: s^2 = \dfrac{\Sigma(x - \bar{x})^2}{n - 1} \\[5ex] (4.)\:\: s^2 = \dfrac{\Sigma f(x - \bar{x})^2}{\Sigma f - 1} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (5.)\:\: s^2 = \dfrac{n(\Sigma x^2) - (\Sigma x)^2}{n(n - 1)} \\[5ex] (6.)\:\: s^2 = \dfrac{\Sigma f(\Sigma fx^2) - (\Sigma fx)^2}{\Sigma f(\Sigma f - 1)} \\[7ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (7.)\;\; s^2 = \dfrac{\Sigma D^2}{n - 1} - \left(\dfrac{\Sigma D}{n - 1}\right)^2 \\[7ex] (8.)\;\; s^2 = \dfrac{\Sigma fD^2}{\Sigma f - 1} - \left(\dfrac{\Sigma fD}{\Sigma f - 1}\right)^2 \\[10ex] \underline{Population\:\:Variance} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (9.)\:\: \sigma^2 = \dfrac{\Sigma(x - \mu)^2}{N} \\[5ex] (10.)\:\: \sigma^2 = \dfrac{\Sigma f(x - \mu)^2}{\Sigma f} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (11.)\:\: \sigma^2 = \dfrac{N(\Sigma x^2) - (\Sigma x)^2}{N^2} \\[5ex] (12.)\:\: \sigma^2 = \dfrac{\Sigma f(\Sigma fx^2) - (\Sigma fx)^2}{(\Sigma f)^2} \\[7ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (13.)\;\; \sigma^2 = \dfrac{\Sigma D^2}{N} - \left(\dfrac{\Sigma D}{N}\right)^2 \\[7ex] (14.)\;\; \sigma^2 = \dfrac{\Sigma fD^2}{\Sigma f} - \left(\dfrac{\Sigma fD}{\Sigma f}\right)^2 \\[10ex] \underline{Sample\:\:Standard\:\:Deviation} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (15.)\:\: s = \sqrt{\dfrac{\Sigma(x - \bar{x})^2}{n - 1}} \\[5ex] (16.)\:\: s = \sqrt{\dfrac{\Sigma f(x - \bar{x})^2}{\Sigma f - 1}} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (17.)\:\: s = \sqrt{\dfrac{n(\Sigma x^2) - (\Sigma x)^2}{n(n - 1)}} \\[5ex] (18.)\:\: s = \sqrt{\dfrac{\Sigma f(\Sigma fx^2) - (\Sigma fx)^2}{\Sigma f(\Sigma f - 1)}} \\[7ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (19.)\;\; s = \sqrt{\dfrac{\Sigma D^2}{n - 1} - \left(\dfrac{\Sigma D}{n - 1}\right)^2} \\[7ex] (20.)\;\; s = \sqrt{\dfrac{\Sigma fD^2}{\Sigma f - 1} - \left(\dfrac{\Sigma fD}{\Sigma f - 1}\right)^2} \\[10ex] \underline{Population\:\:Standard\:\:Deviation} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (21.)\:\: \sigma = \sqrt{\dfrac{\Sigma(x - \mu)^2}{N}} \\[5ex] (22.)\:\: \sigma = \sqrt{\dfrac{\Sigma f(x - \mu)^2}{\Sigma f}} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (23.)\:\: \sigma = \dfrac{\sqrt{N(\Sigma x^2) - (\Sigma x)^2}}{N} \\[5ex] (24.)\:\: \sigma = \dfrac{\sqrt{\Sigma f(\Sigma fx^2) - (\Sigma fx)^2}}{\Sigma f} \\[7ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (25.)\;\; \sigma = \sqrt{\dfrac{\Sigma D^2}{N} - \left(\dfrac{\Sigma D}{N}\right)^2} \\[7ex] (26.)\;\; \sigma = \sqrt{\dfrac{\Sigma fD^2}{\Sigma f} - \left(\dfrac{\Sigma fD}{\Sigma f}\right)^2} \\[10ex] \underline{Range\:\:Rule\:\:of\:\:Thumb} \\[3ex] Approximate\:\:Value\:\:of\:\:Calculating\:\:Standard\:\:Deviation \\[3ex] (27.)\:\: s = \dfrac{Range}{4} = \dfrac{max - min}{4} \\[7ex] \underline{Interquartile\:\:Range} \\[3ex] (28.)\:\: IQR = Q_3 - Q_1 \\[5ex] \underline{Coefficient\:\:of\:\:Variation\:\:for\:\:Sample} \\[3ex] (29.)\:\: CV = \dfrac{s}{x} * 100 ...in\:\:\% \\[7ex] \underline{Coefficient\:\:of\:\:Variation\:\:for\:\:Population} \\[3ex] (30.)\:\: CV = \dfrac{\sigma}{x} * 100 ...in\:\:\% \\[7ex] \underline{Mean\:\:Absolute\:\:Deviation} \\[3ex] (31.)\:\: MAD = \dfrac{\Sigma |x - \bar{x}|}{n} \\[5ex] \underline{Mean\:\:Absolute\:\:Deviation} \\[3ex] (32.)\:\: MAD = \dfrac{\Sigma f|x - \bar{x}|}{\Sigma f} \\[5ex] $



Grouped Data

$ \underline{Class\:\:Midpoint} \\[3ex] (1.)\:\: x_{mid} = \dfrac{LCL + UCL}{2} \\[5ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (2.)\;\; D = x_{mid} - AM \\[5ex] \underline{Sample\:\:Variance} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (3.)\:\: s^2 = \dfrac{\Sigma f(x_{mid} - \bar{x})^2}{\Sigma f - 1} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (4.)\:\: s^2 = \dfrac{\Sigma f(\Sigma fx_{mid}^2) - (\Sigma fx_{mid})^2}{\Sigma f(\Sigma f - 1)} \\[5ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (5.)\;\; s^2 = \dfrac{\Sigma D^2}{n - 1} - \left(\dfrac{\Sigma D}{n - 1}\right)^2 \\[7ex] (6.)\;\; s^2 = \dfrac{\Sigma fD^2}{\Sigma f - 1} - \left(\dfrac{\Sigma fD}{\Sigma f - 1}\right)^2 \\[10ex] \underline{Sample\:\:Standard\:\:Deviation} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (7.)\:\: s = \sqrt{\dfrac{\Sigma f(x_{mid} - \bar{x})^2}{\Sigma f - 1}} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (8.)\:\: s = \sqrt{\dfrac{\Sigma f(\Sigma fx_{mid}^2) - (\Sigma fx_{mid})^2}{\Sigma f(\Sigma f - 1)}} \\[5ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (9.)\;\; s = \sqrt{\dfrac{\Sigma D^2}{n} - \left(\dfrac{\Sigma D}{n - 1}\right)^2} \\[7ex] (10.)\;\; s = \sqrt{\dfrac{\Sigma fD^2}{\Sigma f - 1} - \left(\dfrac{\Sigma fD}{\Sigma f - 1}\right)^2} \\[10ex] \underline{Population\:\:Variance} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (11.)\:\: \sigma^2 = \dfrac{\Sigma f(x_{mid} - \bar{x})^2}{\Sigma f} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (12.)\:\: \sigm^2 = \dfrac{\Sigma f(\Sigma fx_{mid}^2) - (\Sigma fx_{mid})^2}{\Sigma f(\Sigma f)} \\[5ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (13.)\;\; \sigma^2 = \dfrac{\Sigma D^2}{N} - \left(\dfrac{\Sigma D}{N}\right)^2 \\[7ex] (14.)\;\; \sigma^2 = \dfrac{\Sigma fD^2}{\Sigma f} - \left(\dfrac{\Sigma fD}{\Sigma f}\right)^2 \\[10ex] \underline{Population\:\:Standard\:\:Deviation} \\[3ex] \color{red}{First\:\:Formula} \\[3ex] (15.)\:\: \sigma = \sqrt{\dfrac{\Sigma f(x_{mid} - \bar{x})^2}{\Sigma f}} \\[5ex] \color{red}{Second\:\:Formula} \\[3ex] (16.)\:\: \sigma = \sqrt{\dfrac{\Sigma f(\Sigma fx_{mid}^2) - (\Sigma fx_{mid})^2}{\Sigma f(\Sigma f)}} \\[5ex] \underline{Using\;\;Assumed\;\;Mean} \\[3ex] (17.)\;\; \sigma = \sqrt{\dfrac{\Sigma D^2}{N} - \left(\dfrac{\Sigma D}{N}\right)^2} \\[7ex] (18.)\;\; \sigma = \sqrt{\dfrac{\Sigma fD^2}{\Sigma f} - \left(\dfrac{\Sigma fD}{\Sigma f}\right)^2} \\[10ex] $

$z-scores$

A standard unit is how many standard deviations away an observation is from the mean.
A measurement converted to standard units is called a​ z-score.
If an observation has a​ z-score of​ 0, then it is equal to the mean. The mean is 0 standard deviations away from​ itself, so it has a​ z-score of 0.
The​ z-score measures distance from a mean in terms of standard​ deviations, so it can be used to compare values measured in different​ units, such as inches and pounds.

The z-score is:
(1.) Also known as a Standard Score or Standardized Score.

(2.) Defined as the number of standard deviations in which a data value is above or below the mean.

(3.) A measure of location/position because it describes the location of a data value in terms of the standard deviations relative to the mean.

(4.) A positive value if the data value is above the mean.

(5.) A negative value if the data value is below the mean.

(6.) Zero if the data value is the mean.

(7.) Unit less: it does not have a unit.

(8.) Used to determine whether a data value is usual or unusual.

(9.) Used to compare two individual data values measured on the same scale with the same unit of measurement.

(10.) Used to compare two individual data values measured on the same scale with the different units of measurement.

(11.) Used to compare two individual data values measured on the different scales with the same unit of measurement.

(12.) Used to compare two individual data values measured on different scales with different units of measurement.

To explain the aforementioned four points;
In the Education field, one can use $z-score$ to:
compare two scores achieved by the same individual on two different tests
compare scores achieved by two individuals on the same test
compare a score achieved by an individual on a test with the population of scores by different individuals for the same test.

Notable Notes About z-scores

(1.) z-scores are rounded to $2$ decimal places.

(2.) A data value is usual if $-2.00 \le z-score \le 2.00$

(3.) A data value is unusual if $z-score \lt -2.00$ OR $z-score \gt 2.00$

This means that the boundary z-scores to determine whether a data value is usual or unusual are $-2.00$ and $2.00$

Quantiles

Sometimes, it may be necessary to divide a dataset into equal-sized parts.
Quantiles are the data values or cut-off points marking the boundaries between consecutive subsets.
We are interested in these types of Qunatiles:
(1.) Percentiles: divides the dataset into 100 equal parts.
(2.) Deciles: divides the dataset into 10 equal parts.
(3.) Quintiles divides the dataset into 5 equal parts.
(4.) Quartiles divides the dataset into 4 equal parts.
These are measures of location. They indicate the location of data values.
For us to know the exact location of a data value, it is necessary that we arrange the dataset in ascending or descending order.
Arranging it in ascending orer (least to greatest) is highly recommend. This is because one usually begins from the kindergarten up to the 12th grade, not the other way around.
Besides, our formulas will deal with values less than the main value. So, it is important we arrange the data values in ascending order.


Relationship Between Quantiles
Fill in the blank
Percentile Decile Quintile Quartile
10th 1st 📖 📖
20th 2nd 1st 📖
25th 2.5th 1.25th 1st
30th 3rd 📖 1.2nd
40th 📖 2nd 📖
50th 5th 2.5th 2nd
75th 📖 3.75th 3rd
100th 10th 5th 4th


Formulas: Measures of Location

A data value is usual if $-2.00 \le z-score \le 2.00$

A data value is unusual if $z-score \lt -2.00$ OR $z-score \gt 2.00$

$ \underline{Sample} \\[3ex] Minimum\:\:usual\:\:data\:\:value = \bar{x} - 2s \\[3ex] Maximum\:\:usual\:\:data\:\:value = \bar{x} + 2s \\[5ex] \underline{Population} \\[3ex] Minimum\:\:usual\:\:data\:\:value = \mu - 2\sigma \\[3ex] Maximum\:\:usual\:\:data\:\:value = \mu + 2\sigma \\[5ex] \underline{z\:\:score\:\:for\:\:Sample} \\[3ex] (1.)\:\: z = \dfrac{x - \bar{x}}{s} \\[7ex] \underline{z\:\:score\:\:for\:\:Population} \\[3ex] (2.)\:\: z = \dfrac{x - \mu}{\sigma} \\[7ex] \underline{Quantiles(Percentiles,\:Deciles,\:Quintiles,\:and\:Quartiles)} \\[3ex] \color{red}{Convert\:\:a\:\:Data\:\:value\:\:to\:\:a\:\:Quantile} \\[3ex] x\:\:and\:\:y\:\:are\:\:two\:\:different\:\:variables \\[3ex] (3.)\:\: Percentile\:\:of\:\:x = \dfrac{number\:\:of\:\:values\:\:less\:\:than\:\:x}{total\:\:number\:\:of\:\:values} * 100 = yth\:\:Percentile \\[5ex] (4.)\:\: Decile\:\:of\:\:x = \dfrac{number\:\:of\:\:values\:\:less\:\:than\:\:x}{total\:\:number\:\:of\:\:values} * 10 = yth\:\:Decile \\[5ex] (5.)\:\: Quintile\:\:of\:\:x = \dfrac{number\:\:of\:\:values\:\:less\:\:than\:\:x}{total\:\:number\:\:of\:\:values} * 5 = yth\:\:Quintile \\[5ex] (6.)\:\: Quartile\:\:of\:\:x = \dfrac{number\:\:of\:\:values\:\:less\:\:than\:\:x}{total\:\:number\:\:of\:\:values} * 4 = yth\:\:Quartile \\[7ex] \color{red}{Convert\:\:a\:\:Quantile\:\:to\:\:a\:\:Data\:\:Value} \\[3ex] Calculate\:\:the\:\:xth\:\:position\:\:of\:\:the\:\:yth\:\:Quantile \\[3ex] (7.)\:\: xth\:\:position = \dfrac{yth\:\:Percentile}{100} * total\:\:number\:\:of\:\:values \\[5ex] (8.)\:\: xth\:\:position = \dfrac{yth\:\:Decile}{10} * total\:\:number\:\:of\:\:values \\[5ex] (9.)\:\: xth\:\:position = \dfrac{yth\:\:Quintile}{5} * total\:\:number\:\:of\:\:values \\[5ex] (10.)\:\: xth\:\:position = \dfrac{yth\:\:Quartile}{4} * total\:\:number\:\:of\:\:values \\[7ex] $

If the $xth$ position then,
is an integer
$xth\:\:position = \dfrac{xth\:\:position + (x + 1)th\:\;position}{2}$

In other words, find the value of the $xth$ position; find the value of the next position; and determine the mean of the two values.
is not an integer $xth$ position is rounded up


$ \underline{The\:\:Five-Number\:\:Summary\:\:of\:\:Data} \\[3ex] (11.)\:\: Minimum\:(min) \\[3ex] (12.)\:\: Lower\:\:Quartile\:(Q_1) \\[3ex] (13.)\:\: Median\:\:or\:\:Middle\:\:Quartile\:(Q_2) \\[3ex] (14.)\:\: Upper\:\:Quartile\:(Q_3) \\[3ex] (15.)\:\: Maximum\:(Max) \\[5ex] \underline{Other\:\:Statistics\:\:from\:\:Quantiles} \\[3ex] (16.)\:\: IQR = Q_3 - Q_1 \\[3ex] (17.)\:\: SIQR = \dfrac{IQR}{2} = \dfrac{Q_3 - Q_1}{2} \\[5ex] (18.)\:\: MQ = \dfrac{Q_3 + Q_1}{2} \\[5ex] (19.)\:\: Upper\:\:Quartile\:(Q_3) \\[3ex] (20.)\:\: LF = Q_1 - 1.5(IQR) \\[3ex] (21.)\:\: UF = Q_3 + 1.5(IQR) $



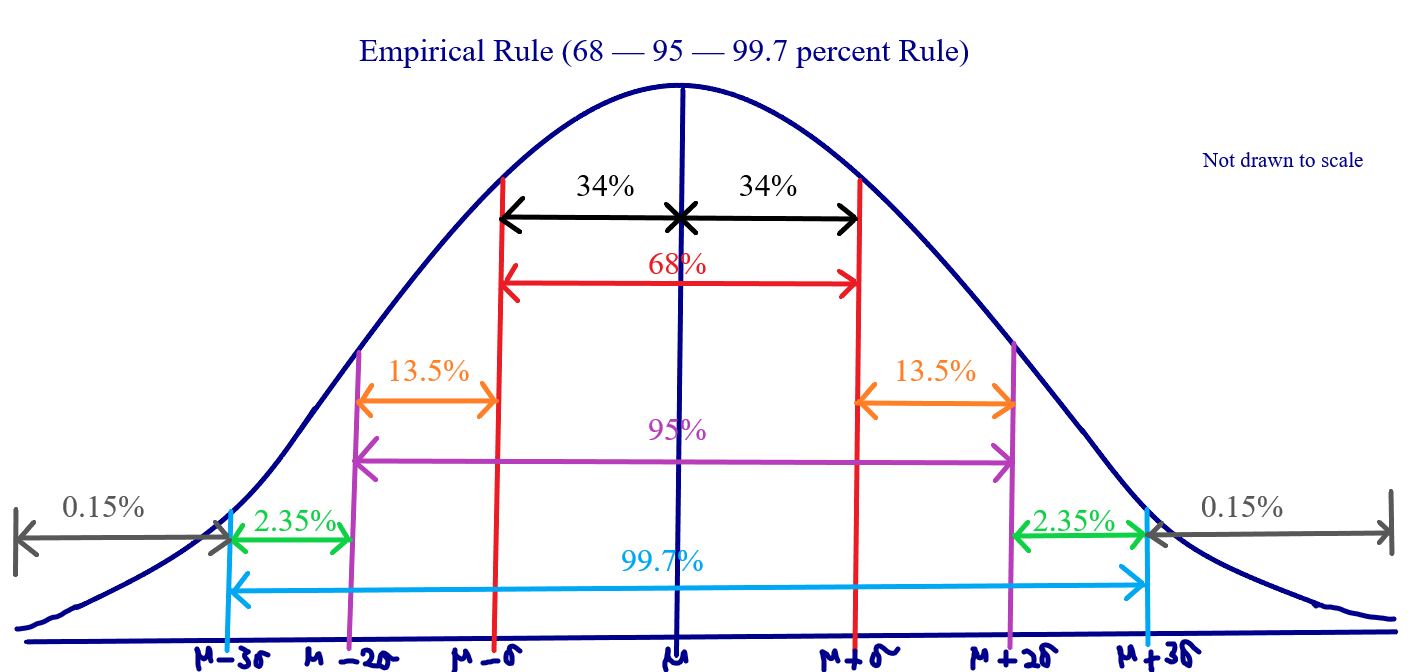
Empirical Rule

The Empirical Rule also known as the 68–95–99.7 percent Rule applies to distributions that are unimodal and​ symmetric.
It states that:
In a unimodal symmetric distribution (normal distribution) dataset, approximately:
(a.) 68% of the distribution lie within (below and above) one standard deviation from the mean
(b.) 95% of the distribution lie within (below and above) two standard deviations from the mean
(c.) 99.7% of the distribution lie within (below and above) three standard deviations from the mean

In other words, in a unimodal normal distribution (bell-shaped curve distribution):
(a.) 68% of the distribution lie from    μ − σ    to    μ + σ
(a.) 95% of the distribution lie from    μ − 2σ    to    μ + 2σ
(a.) 99.7% of the distribution lie from    μ − 3σ    to    μ + 3σ

Let us review an example:
Empirical Rule

Example: Assume the average height and the standard deviation of basketball players in the a certain school is 175cm and 7cm respectively.
Describe/Analyze this information using the Empirical Rule.

Solution:
mean = 175cm
standard deviation = 7cm

mean + 1 standard deviation = 175 + 7 = 182cm
mean − 1 standard deviation = 175 − 7 = 168cm
mean + 2 standard deviations = 175 + 2(7) = 175 + 14 = 189cm
mean − 2 standard deviations = 175 − 2(7) = 175 − 14 = 161cm
mean + 3 standard deviations = 175 + 3(7) = 175 + 21 = 196cm
mean − 3 standard deviations = 175 − 3(7) = 175 − 21 = 154cm

68% of the heights lie between 168cm and 182cm
95% of the heights lie between 161cm and 189cm
99.7% of the heights lie between 154cm and 196cm
34% of the heights lie between 168cm and 175cm
34% of the heights lie between 175cm and 182cm
47.5% of the heights lie between 161cm and 175cm
47.5% of the heights lie between 175cm and 189cm
49.85% of the heights lie between 154cm and 175cm
49.85% of the heights lie between 175cm and 196cm
50% lie below 175cm
50% lie above 175cm
16% lie below 168cm
16% lie above 182cm
2.5% lie below 161cm
2.5% lie above 189cm
0.15% lie below 154cm
0.15% lie above 196cm
2.35% lie between 154cm and 161cm
2.35% lie between 189cm and 196cm
13.5% lie between 161cm and 168cm
13.5% lie between 182cm and 189cm
15.85% lie between 154cm and 168cm
15.85% lie between 182cm and 196cm
84% lie above 168cm
84% lie below 182cm
83.85% lie between 168cm and 196cm
83.85% lie between 154cm and 182cm
81.5% lie between 168cm and 189cm
81.5% lie between 161cm and 182cm
97.5% lie above 161cm
97.5% lie below 189cm
97.35% lie between 161cm and 196cm
97.35% lie between 154cm and 189cm
99.85% lie above 154cm
99.85% lie below 196cm

Normal Distribution Tables

Standard Normal Distribution Table (Left-Shaded Area)
Normal Distribution Area: Left Shaded: Negative Normal Distribution Area: Left Shaded: Positive



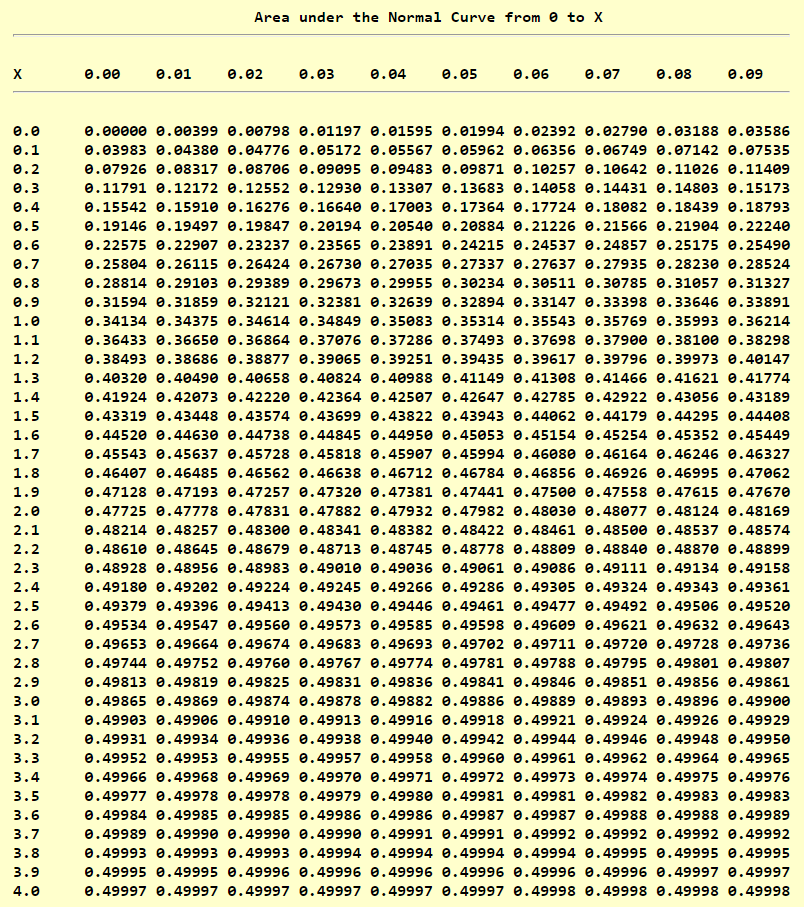
Standard Normal Distribution Table (Center-Shaded Area)
Normal Distribution Area: Center Shaded

Normal Distribution Table: Center Shaded



Boxplots

A boxplot (also known as a box-and-whisker plot):
(1.) is a graphical representation of data using the five-number summary of data.
It help us to visualize the location of the​ five-number summary.

(2.) is a useful graphical tool for visualizing a​ distribution, especially when comparing two or more groups of data.

(3.) shows us the distribution divided into fourths.

Boxplots are best used only for unimodal distributions because they hide bimodality or any multimodality.
Hence, they are not recommended for use with bimodal or multimodal distributions.
The left edge of the box is at the first quartile​ (Q1).
The right edge is at the third quartile​ (Q3).
Thus the middle​ 50% of the sorted observations lie inside the box.​
Therefore, the length of the box is proportional to the Interquartile Range (IQR).
In a​ boxplot, the vertical line inside the box marks the location of the median.

The boxplot also identifiers the outliers of a dataset.
Outliers are observations that are a distance of more than 1.5 interquartile ranges below the first quartile​ (the left edge of a horizontal​ box) or above the third quartile​ (the right​ edge); these are typically called the left limit (lower fence) and the right​ limit (upper fence), respectively.
To see potential​ outliers, the whiskers are drawn from the edge of each box to the most extreme observation that is not a potential outlier.
Recap: In a​ boxplot, the whiskers extend to the most extreme values that are not potential outliers.
Potential outliers are then represented by others​ markers, such as dots.
This implies that before we can draw the​ whiskers, we must identify any potential outliers.
For the boxplot to be used to represent any dataset, it must mark all potential outliers.
The first step with potential outliers is always to investigate.
A potential outlier might not be an outlier at all. It might tell an interesting​ story, or it might be the result of an error in entering data.



Multiple boxplots are boxplots of several datasets usually constructed on the same scale.
Modified boxplots are boxplots in which the outliers are identified with points or asterisks, and in which the solid horizontal line extends only to the minimum and maximum value that are not outliers.



Outliers and Fences

An outlier is an extreme data value: a data value that is either too low or too high from the majority of the other values in a dataset.
It affects several statistics of data including the mean and the standard deviation among others.
Fences are cutoffs for determining outliers.

Ask students to write the formulas for the lower fence and the upper fence.

A data value is an outlier if:
(1.) It is less than the lower fence OR
(2.) It is greater than the upper fence.
So, an outlier can also be defined as a data value which falls more than 1.5 times the interquartile range: below the lower quartile or above the upper quartile.



References

Chukwuemeka, Samuel Dominic (2023). Descriptive Statistics. Retrieved from https://statistical-science.appspot.com/

Black, Ken. (2012). Business Statistics for Contemporary Decision Making (7th ed.). New Jersey: Wiley

Gould, R., Wong, R., & Ryan, C. N. (2020). Introductory Statistics: Exploring the world through data (3rd ed.). Pearson.

Kozak, Kathryn. (2015). Statistics Using Technology (2nd ed.).

OpenStax, Introductory Statistics.OpenStax CNX. Sep 28, 2016. Retrieved from https://cnx.org/contents/30189442-6998-4686-ac05-ed152b91b9de@18.12

Sullivan, M., & Barnett, R. (2013). Statistics: Informed decisions using data with an introduction to mathematics of finance (2nd custom ed.). Boston: Pearson Learning Solutions.

Triola, M. F. (2015). Elementary Statistics using the TI-83/84 Plus Calculator (5th ed.). Boston: Pearson

Triola, M. F. (2022). Elementary Statistics. (14th ed.) Hoboken: Pearson.

Weiss, Neil A. (2015). Elementary Statistics (9th ed.). Boston: Pearson

CrackACT. (n.d.). Retrieved from http://www.crackact.com/act-downloads/

CMAT Question Papers CMAT Previous Year Question Bank - Careerindia. (n.d.). Https://Www.Careerindia.Com. Retrieved May 30, 2020, from https://www.careerindia.com/entrance-exam/cmat-question-papers-e23.html

CSEC Math Tutor. (n.d). Retrieved from https://www.csecmathtutor.com/past-papers.html

Datasets - Data.gov. (2012). Data.Gov. https://catalog.data.gov/dataset

DLAP Website. (n.d.). Curriculum.gov.mt. https://curriculum.gov.mt/en/Examination-Papers/Pages/list_secondary_papers.aspx

Free Jamb Past Questions And Answer For All Subject 2020. (2020, January 31). Vastlearners. https://www.vastlearners.com/free-jamb-past-questions/

Geogebra. (2019). Graphing Calculator - GeoGebra. Geogebra.org. https://www.geogebra.org/graphing?lang=en

GCSE Exam Past Papers: Revision World. Retrieved April 6, 2020, from https://revisionworld.com/gcse-revision/gcse-exam-past-papers

HSC exam papers | NSW Education Standards. (2019). Nsw.edu.au. https://educationstandards.nsw.edu.au/wps/portal/nesa/11-12/resources/hsc-exam-papers

JAMB Past Questions, WAEC, NECO, Post UTME Past Questions. (n.d.). Nigerian Scholars. Retrieved February 12, 2022, from https://nigerianscholars.com/past-questions/

KCSE Past Papers by Subject with Answers-Marking Schemes. (n.d.). ATIKA SCHOOL. Retrieved June 16, 2022, from https://www.atikaschool.org/kcsepastpapersbysubject

Myschool e-Learning Centre - It's Time to Study! - Myschool. (n.d.). https://myschool.ng/classroom

Netrimedia. (2022, May 2). ICSE 10th Board Exam Previous Papers- Last 10 Years. Education Observer. https://www.educationobserver.com/icse-class10-previous-papers/

NSC Examinations. (n.d.). www.education.gov.za. https://www.education.gov.za/Curriculum/NationalSeniorCertificate(NSC)Examinations.aspx

School Curriculum and Standards Authority (SCSA): K-12. Past ATAR Course Examinations. Retrieved December 10, 2021, from https://senior-secondary.scsa.wa.edu.au/further-resources/past-atar-course-exams

West African Examinations Council (WAEC). Retrieved May 30, 2020, from https://waeconline.org.ng/e-learning/Mathematics/mathsmain.html

Papua New Guinea: Department of Education. (n.d.). www.education.gov.pg. Retrieved November 24, 2020, from http://www.education.gov.pg/TISER/exams.html

51 Real SAT PDFs and List of 89 Real ACTs (Free) : McElroy Tutoring. (n.d.). Mcelroytutoring.com. Retrieved December 12, 2022, from https://mcelroytutoring.com/lower.php?url=44-official-sat-pdfs-and-82-official-act-pdf-practice-tests-free