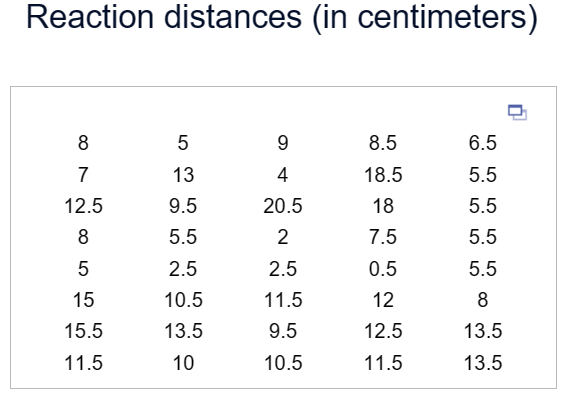
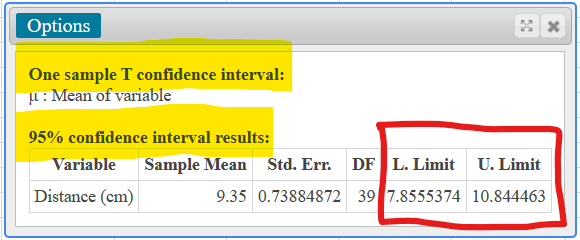
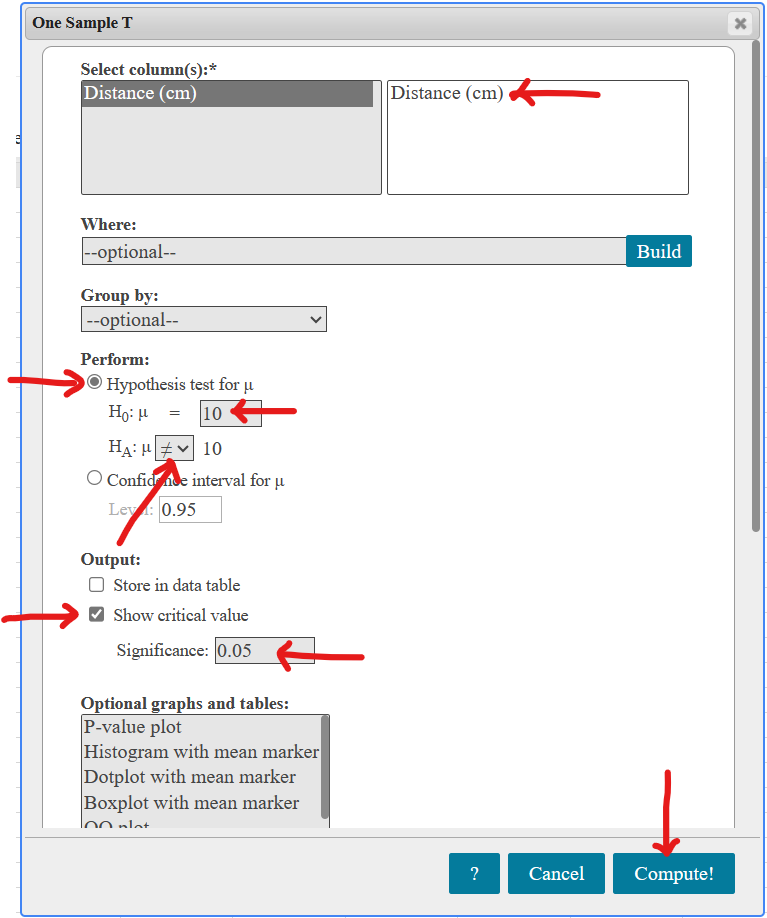
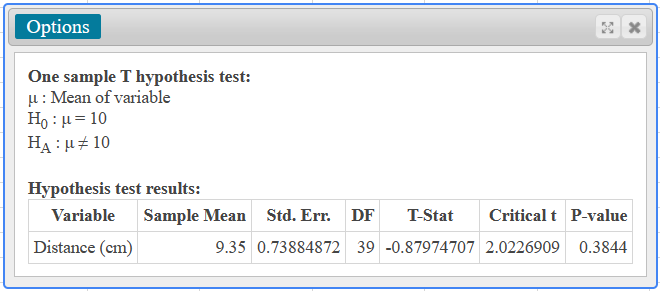
(1.) 
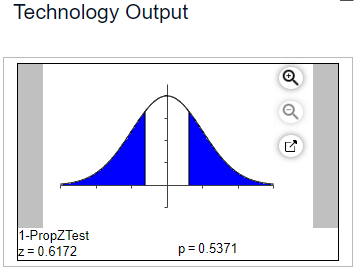
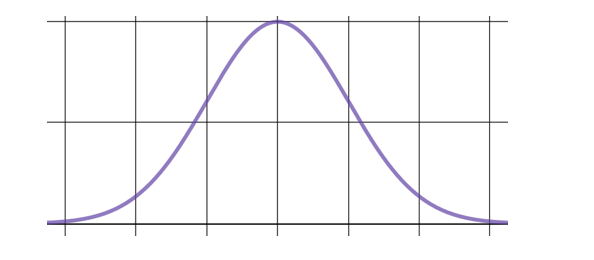
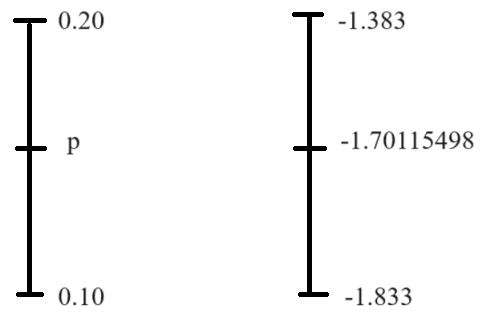
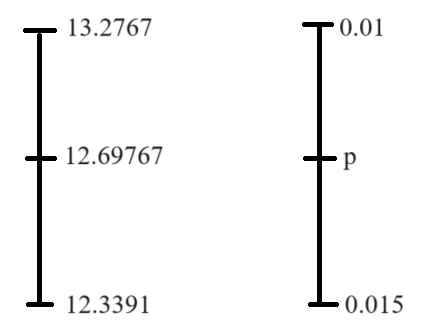
Assume the curve is used for a two-tailed hypothesis test.
The p-value is 0.0888
(a.) If the two-tailed test was conducted at a 5% significance level, would you reject the null hypothesis OR fail to reject the null hypothesis?
(b.) If the two-tailed test was conducted at a 10% level of significance, would you reject the null hypothesis OR fail to reject the null hypothesis?
(c.) If we decided to do a right-tailed test instead at a 5% significance level, would you reject the null hypothesis OR fail to reject the null hypothesis?
$ (a.) \\[3ex] Two-tailed\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] 0.0888 \gt 0.05 \\[3ex] p-value \gt \alpha \\[3ex] $ Decision: Fail to reject the null hypothesis
$ (b.) \\[3ex] Two-tailed\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] 0.0888 \le 0.1 \\[3ex] p-value \le \alpha \\[3ex] $ Decision: Reject the null hypothesis
$ (c.) \\[3ex] One-tail\:(Right-tailed)\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] 0.0888 \gt 0.05 \\[3ex] p-value \gt \alpha \\[3ex] $ Decision: Fail to reject the null hypothesis

Assume the curve is used for a two-tailed hypothesis test.
The p-value is 0.0888
(a.) If the two-tailed test was conducted at a 5% significance level, would you reject the null hypothesis OR fail to reject the null hypothesis?
(b.) If the two-tailed test was conducted at a 10% level of significance, would you reject the null hypothesis OR fail to reject the null hypothesis?
(c.) If we decided to do a right-tailed test instead at a 5% significance level, would you reject the null hypothesis OR fail to reject the null hypothesis?
$ (a.) \\[3ex] Two-tailed\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] 0.0888 \gt 0.05 \\[3ex] p-value \gt \alpha \\[3ex] $ Decision: Fail to reject the null hypothesis
$ (b.) \\[3ex] Two-tailed\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] 0.0888 \le 0.1 \\[3ex] p-value \le \alpha \\[3ex] $ Decision: Reject the null hypothesis
$ (c.) \\[3ex] One-tail\:(Right-tailed)\:\:Hypothesis\:\:Test \\[3ex] p-value = 0.0888 \\[3ex] \alpha = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] 0.0888 \gt 0.05 \\[3ex] p-value \gt \alpha \\[3ex] $ Decision: Fail to reject the null hypothesis
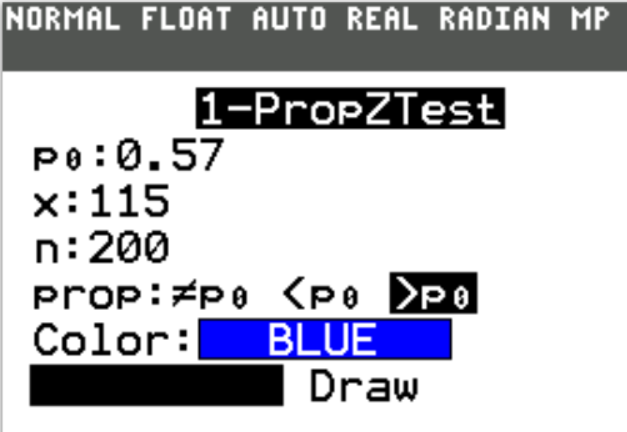
(2.) Claim: Fewer than 97% of adults have a cell phone.
In a reputable poll of 1217 adults, 89% said that they have a cell phone.
Find the value of the test statistic.
(Round to two decimal places as needed.)
One-Sample Proportion
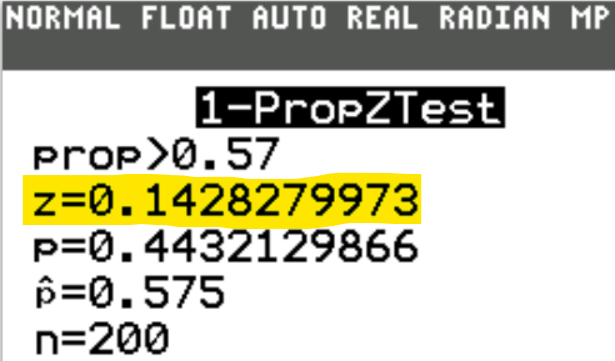
$ H_0:\;\; p = 97\% = 0.97 \\[3ex] q = 1 - p = 1 - 0.97 = 0.03 \\[5ex] n = 1217 \\[3ex] \hat{p} = 89\% = 0.89 \\[3ex] z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{pq}{n}}} \\[9ex] z = \dfrac{0.89 - 0.97}{\sqrt{\dfrac{0.97(0.03)}{1217}}} \\[9ex] z = -16.36020652 \\[3ex] z \approx -16.36 $
In a reputable poll of 1217 adults, 89% said that they have a cell phone.
Find the value of the test statistic.
(Round to two decimal places as needed.)
One-Sample Proportion
$ H_0:\;\; p = 97\% = 0.97 \\[3ex] q = 1 - p = 1 - 0.97 = 0.03 \\[5ex] n = 1217 \\[3ex] \hat{p} = 89\% = 0.89 \\[3ex] z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{pq}{n}}} \\[9ex] z = \dfrac{0.89 - 0.97}{\sqrt{\dfrac{0.97(0.03)}{1217}}} \\[9ex] z = -16.36020652 \\[3ex] z \approx -16.36 $