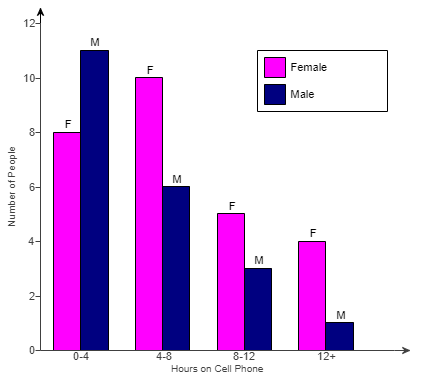
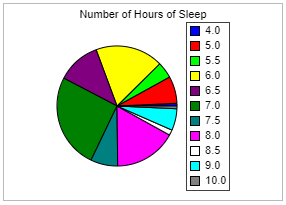
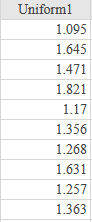
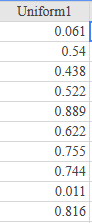
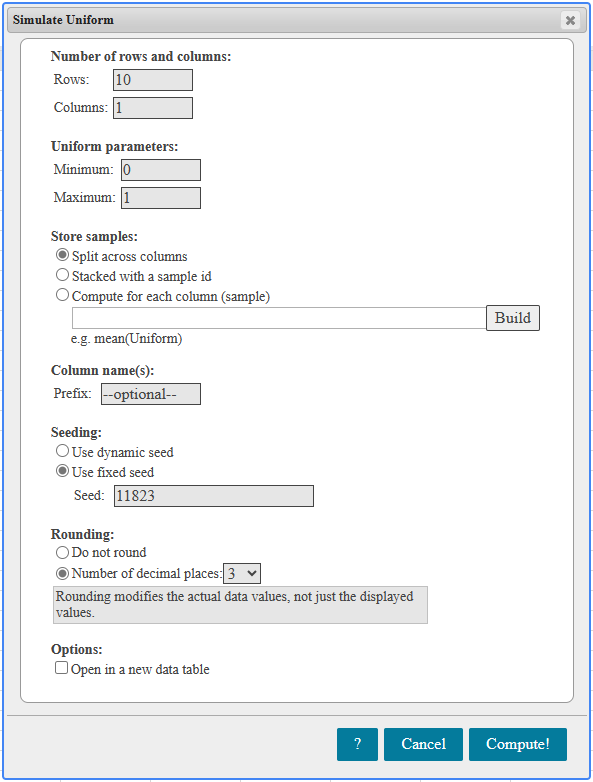
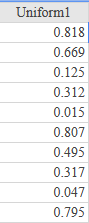
(5.) GCSE Here is some information, by ticket type, about the number of people visiting a cinema
one week.
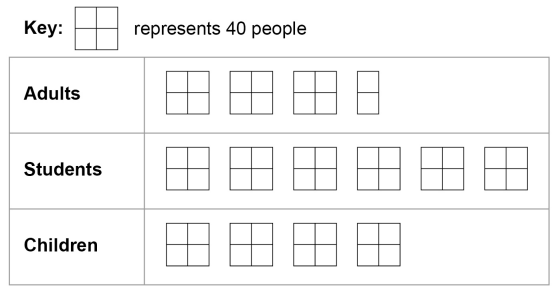
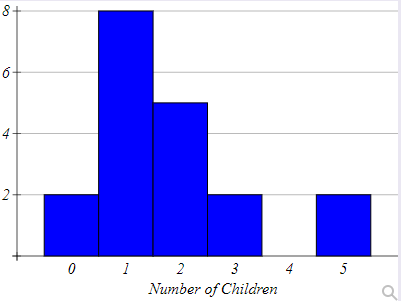
(a) How many children visited the cinema?
(b) How many more students than adults visited the cinema?
(c) A bar chart is drawn to show the number of people visiting the cinema one month.
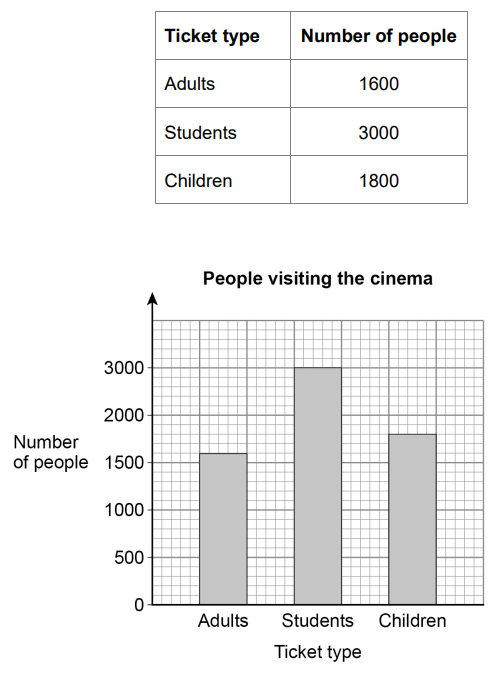
Give one criticism of the bar chart.
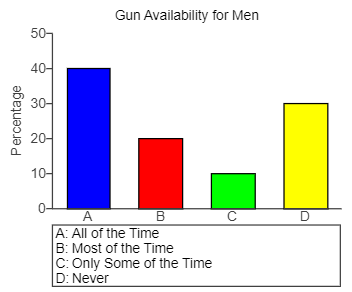
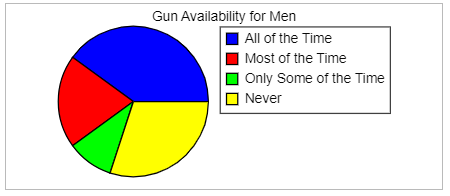
$ Key:\;\;1\;box = 40\;people \\[3ex] (a) \\[3ex] Number\;\;of\;\;children \\[3ex] = 4\;boxes \\[3ex] = 4(40) \\[3ex] = 160\;people \\[3ex] (b) \\[3ex] Number\;\;of\;\;students \\[3ex] = 6\;boxes \\[3ex] = 6(40) \\[3ex] = 240\;people \\[3ex] Number\;\;of\;\;adults \\[3ex] = 3\dfrac{1}{2}\;boxes \\[5ex] = \dfrac{7}{2}(40) \\[5ex] = 7(20) \\[3ex] = 140\;people \\[3ex] More\;\;students\;\;than\;\;adults \\[3ex] = students - adults \\[3ex] = 240 - 140 \\[3ex] = 100\;people \\[3ex] $ (c)
The scale on the vertical axis (Number of people) is incorrect because 2500 is missing.
This implies that the number of Students is not represented correctly on the bar chart.

(a) How many children visited the cinema?
(b) How many more students than adults visited the cinema?
(c) A bar chart is drawn to show the number of people visiting the cinema one month.

Give one criticism of the bar chart.
$ Key:\;\;1\;box = 40\;people \\[3ex] (a) \\[3ex] Number\;\;of\;\;children \\[3ex] = 4\;boxes \\[3ex] = 4(40) \\[3ex] = 160\;people \\[3ex] (b) \\[3ex] Number\;\;of\;\;students \\[3ex] = 6\;boxes \\[3ex] = 6(40) \\[3ex] = 240\;people \\[3ex] Number\;\;of\;\;adults \\[3ex] = 3\dfrac{1}{2}\;boxes \\[5ex] = \dfrac{7}{2}(40) \\[5ex] = 7(20) \\[3ex] = 140\;people \\[3ex] More\;\;students\;\;than\;\;adults \\[3ex] = students - adults \\[3ex] = 240 - 140 \\[3ex] = 100\;people \\[3ex] $ (c)
The scale on the vertical axis (Number of people) is incorrect because 2500 is missing.
This implies that the number of Students is not represented correctly on the bar chart.
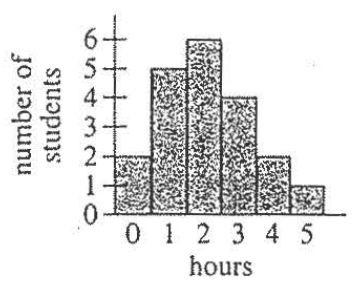
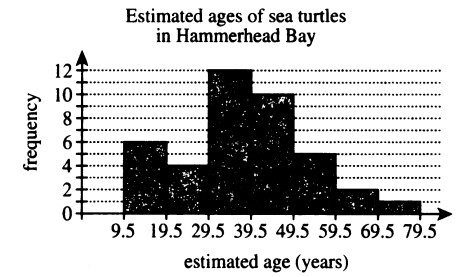
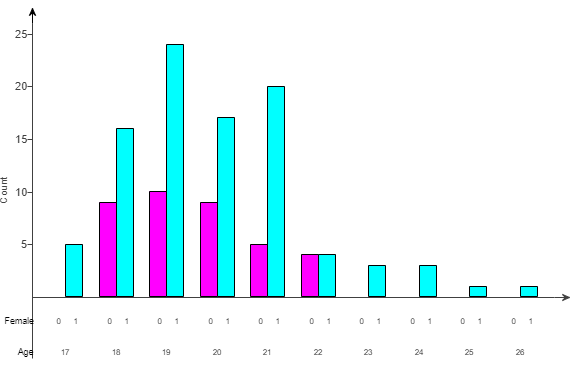
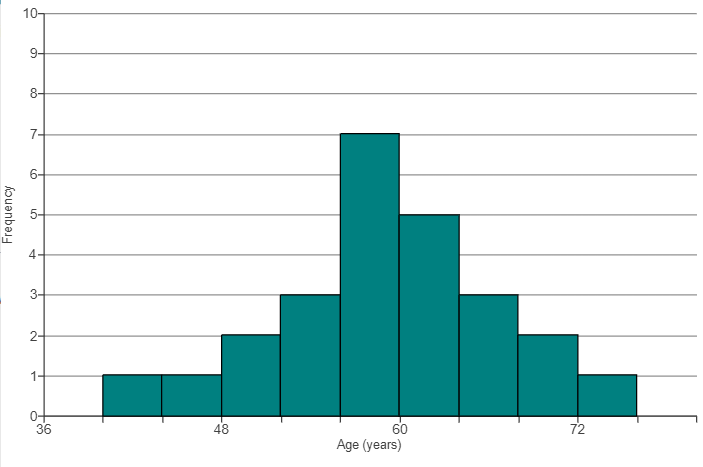
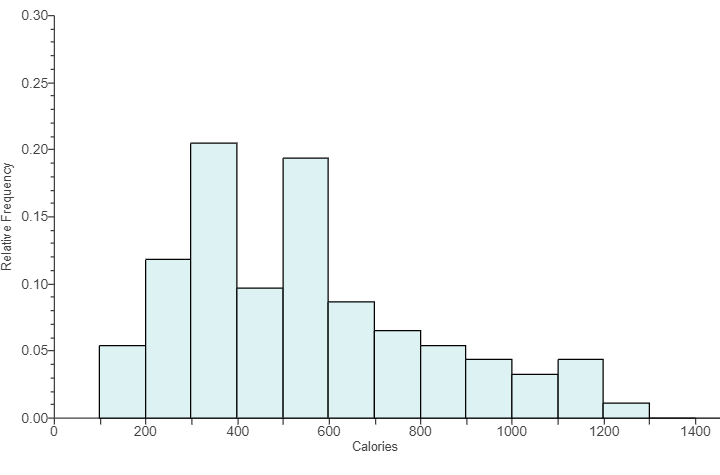
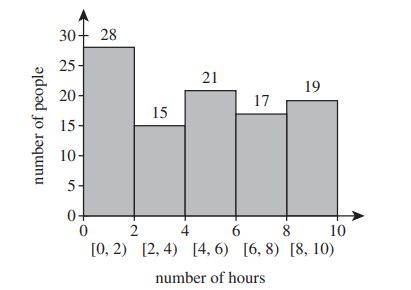
(6.) ACT The histogram below shows the results of a survey of 100 people.
Each person identified the number of hours per week that they watch TV.
How many people surveyed watch TV at least 4 hours per week?
$ F.\;\; 57 \\[3ex] G.\;\; 38 \\[3ex] H.\;\; 28 \\[3ex] J.\;\; 21 \\[3ex] K.\;\; 19 \\[3ex] $
At least 4 hours means 4 hours or more (≥4)
$ Number\;\;who\;\;watch\;\;TV\;\;\ge 4\;hours/week \\[3ex] = 21 + 17 + 19 \\[3ex] = 57\;people $
Each person identified the number of hours per week that they watch TV.
How many people surveyed watch TV at least 4 hours per week?

$ F.\;\; 57 \\[3ex] G.\;\; 38 \\[3ex] H.\;\; 28 \\[3ex] J.\;\; 21 \\[3ex] K.\;\; 19 \\[3ex] $
At least 4 hours means 4 hours or more (≥4)
$ Number\;\;who\;\;watch\;\;TV\;\;\ge 4\;hours/week \\[3ex] = 21 + 17 + 19 \\[3ex] = 57\;people $